Abstract
Unraveling the secrets of how much nonstabilizerness a quantum dynamic can generate is crucial for harnessing the power of magic states, the essential resources for achieving quantum advantage and realizing fault-tolerant quantum computation. In this work, we introduce the amortized α-stabilizer Rényi entropy, a magic monotone for unitary operations that quantifies the nonstabilizerness generation capability of quantum dynamics. Amortization is key in quantifying the magic of quantum dynamics, as we reveal that nonstabilizerness generation can be enhanced by prior nonstabilizerness in input states when considering the α-stabilizer Rényi entropy, while this is not the case for robustness of magic or stabilizer extent. We demonstrate the versatility of the amortized α-stabilizer Rényi entropy in investigating the nonstabilizerness resources of quantum dynamics of computational and fundamental interest. In particular, we establish improved lower bounds on the T-count of quantum Fourier transforms and the quantum evolutions of one-dimensional Heisenberg Hamiltonians, showcasing the power of this tool in studying quantum advantages and the corresponding cost in fault-tolerant quantum computation.
Publication
arXiv:2409.06659

PhD Student (2023)
I obtained my BS in Applied Mathematics from China Agricultural University under the supervision of Prof. Zhencai Shen. I obtained my MS degree in Cyberspace Security from University of Chinese Academy of Sciences under the supervision of Prof. Zhenyu Huang. My research interests include quantum information theory and quantum computation.

Research Associate
I obtained my BS in Mathematics and Applied Mathematics from University of Science and Technology of China. I obtained my PhD degree in Applied Mathematics from University of Chinese Academy of Sciences under the supervision of Prof. Xiao-Shan Gao. My research interests include quantum computing, symbolic computation and cryptanalysis.



Associate Professor
Prof. Xin Wang founded the QuAIR lab at HKUST(Guangzhou) in June 2023. His research primarily focuses on better understanding the limits of information processing with quantum systems and the power of quantum artificial intelligence. Prior to establishing the QuAIR lab, Prof. Wang was a Staff Researcher at the Institute for Quantum Computing at Baidu Research, where he concentrated on quantum computing research and the development of the Baidu Quantum Platform. Notably, he spearheaded the development of Paddle Quantum, a Python library designed for quantum machine learning. From 2018 to 2019, Prof. Wang held the position of Hartree Postdoctoral Fellow at the Joint Center for Quantum Information and Computer Science (QuICS) at the University of Maryland, College Park. He earned his doctorate in quantum information from the University of Technology Sydney in 2018, under the guidance of Prof. Runyao Duan and Prof. Andreas Winter. In 2014, Prof. Wang obtained his B.S. in mathematics (with Wu Yuzhang Honor) from Sichuan University.
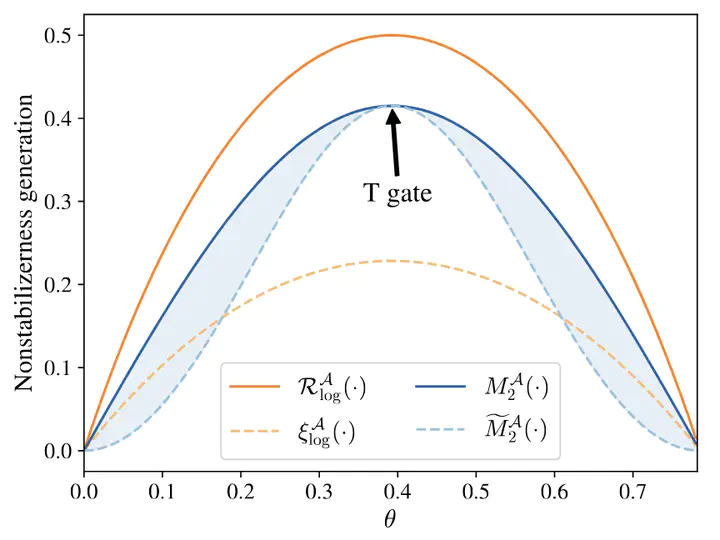 Sketches that characterizes the maximum nonstabilizerness generation.
Sketches that characterizes the maximum nonstabilizerness generation.