Paddle Quantum Quick Start Manual¶
Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
Overview¶
Quantum computing (QC) is a new computing model laying in the intersection of quantum mechanics and theory of computation. QC follows the fundamental laws of quantum theory to manipulate quantum bits (qubits). For many specific computational tasks, it is widely believed that quantum algorithms exhibit advantages over classical algorithms at least in theory. For a systematic introduction to the subject of QC, we refer to [1-2].
In recent years, one of the popular research topics in QC is combining the potential of quantum computing and artificial intelligence. Quantum machine learning (QML) is such an interdisciplinary subject. Researchers want to utilize the information processing advantages of quantum computing to promote the development of artificial intelligence. On the other side, it is also worth exploring the possibility of using artificial intelligence technology to break through the bottleneck of quantum computing research and development. For introductory materials about quantum machine learning, please refer to [3-5].
Here, we provide a quick start for users to get started with Paddle Quantum. Currently, you can read all the content online or download the Jupyter Notebook from our GitHub. In terms of content, the quick start includes the following sections:
- Introduction to quantum computing and quantum neural network (QNN)
- Introduction to Paddle Quantum
- PaddlePaddle optimizer tutorial
- A case study on quantum machine learning - Variational Quantum Eigensolver (VQE)
Latest version updated on: Dec. 3rd, 2021 by Paddle Quantum developers.
Quantum Computing Fundamentals¶
Quantum Computing (QC) uses unique phenomena in quantum physics (quantum superposition, quantum interference, and quantum entanglement) to design algorithms and help solve specific tasks in physics, chemistry, and optimization theory. There are several existing quantum computation models including the Adiabatic Quantum Computation (AQC) based on the adiabatic theorem and Measurement-Based Quantum Computation (MBQC). This introduction will focus on the most widely used Quantum Circuit model. In quantum circuits, the basic computation unit is the quantum bit (qubit), which is similar to the concept of bit in classical computers. Classical bits can only be in one of the two states, 0 or 1. By comparison, qubits can not only be in states $|0\rangle$ and $|1\rangle$ but also in a superposition state (we will explain this concept later). Quantum circuit model utilize quantum logic gates to manipulate the states of these qubits. The mathematics behind this process is linear algebra in the complex domain. Here we assume the readers are already familiar with linear algebra.
What is a qubit?¶
Mathematical representation¶
In quantum mechanics, the state of a two-level quantum system (e.g. electron spin) can be expressed as a state vector obtained through linear combinations of the following orthonormal basis,
$$ |0\rangle := \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad |1\rangle := \begin{bmatrix} 0 \\ 1 \end{bmatrix}. \tag{1} $$The vector representation here follows the Dirac notation (bra-ket) in quantum physics. This orthonormal basis $\{|0\rangle, |1\rangle \}$ is known as the computational basis. Physically, one could consider $|0\rangle$ and $|1\rangle$ as the energy ground state and excited state of an atom, respectively. All possible pure states of a qubit can be regarded as normalized vectors in the two-dimensional Hilbert space. Moreover, multi-qubit states can be represented by unit vectors in high-dimensional Hilbert space where the basis is the tensor product of $\{|0\rangle, |1\rangle\}$. For example, a 2-qubit quantum state can be represented by a unit complex vector in a 4-dimensional Hilbert space with the orthonormal basis,
$$ \left\{ |00\rangle = |0\rangle\otimes |0\rangle := \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \quad |01\rangle = |0\rangle\otimes |1\rangle := \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \quad |10\rangle = |1\rangle\otimes |0\rangle := \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \quad |11\rangle = |1\rangle\otimes |1\rangle := \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right\}. \tag{2} $$By convention, the leftmost position in ket notation represents the first qubit $q_0$, the second position represents the second qubit $q_1$, and so on. The symbol $\otimes$ denotes the tensor product operation. It works as follows: Given two matrices $A_{m\times n}$ and $B_{p \times q}$, then the tensor product of $A, B$ is
$$ A \otimes B = \begin{bmatrix} a_{11}B & \cdots & a_{1 n}B\\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{m n}B \end{bmatrix}_{(mp)\times (nq)}. \tag{3} $$Any single qubit quantum state $|\psi\rangle$ can be written as a linear combination (superposition) of the basis vectors $|0\rangle$ and $|1\rangle$.
$$ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle := \begin{bmatrix} \alpha \\ \beta \end{bmatrix}. \tag{4} $$where $\alpha$ and $\beta$ are complex numbers referred as the probability amplitudes. According to Born Rule, the probability to find the qubit in $|0\rangle$ state is $|\alpha|^2$; and the probability of $|1\rangle$ is $|\beta|^2$. Since the sum of probabilities equals to 1, one should introduce the constraint: $|\alpha|^2 + |\beta|^2 = 1$.
Bloch sphere representation¶
Bloch sphere is a clever tool for visualizing single qubit states (pure). The point on the sphere represent the possible quantum states of a single qubit. (see Figure.1)
$$ |\psi\rangle = \alpha |0\rangle + \beta |1\rangle = \cos\bigg(\frac{\theta}{2}\bigg) |0\rangle + e^{i\varphi}\sin\bigg(\frac{\theta}{2}\bigg) |1\rangle. \tag{5} $$For a classical bit in state $|0\rangle$ or $|1\rangle$ , it corresponds to the north or south pole of the Bloch sphere. A qubit state can be not only $|0\rangle$ or $|1\rangle$ but also the superposition state of $|0\rangle$ and $|1\rangle$. So any point on the sphere corresponds to a quantum state.
For example, the quantum state $\frac{1}{\sqrt{2}}\big(|0\rangle + i|1\rangle\big)$ is at the intersection of the equator and $+y$ axis.
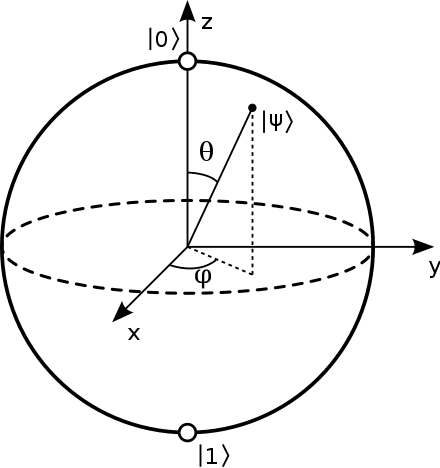
Figure.1
Bloch sphere representation of single qubit. [Image source]
Note: The compound system of multiple qubits cannot be represented by Bloch sphere.
Example: how to display the single qubit quantum state on the Bloch sphere?¶
Taking the output state of random unitary gate as an example, we show how to use the built-in function of Paddle Quantum to draw Bloch sphere. In this example, we use random rotation angles to construct random unitary operators. Let the initialized quantum circuit pass through this unitary operator, we can get the final state of the quantum circuit. This final state is a random quantum state. In this way, the sampling is repeated many times to generate a list of quantum states. By inputting them into the Bloch sphere by using the function of visual package in the Paddle Quantum, the display of single qubit quantum state on the Bloch sphere can be realized.
The specific codes are as follows:
import numpy as np
import paddle
import paddle_quantum
from paddle import matmul, transpose, trace
from paddle_quantum.ansatz import Circuit
from paddle_quantum.state import State
from paddle_quantum.linalg import dagger
from paddle_quantum.qinfo import random_pauli_str_generator, pauli_str_to_matrix
from paddle_quantum.visual import plot_state_in_bloch_sphere, plot_rotation_in_bloch_sphere
import warnings
warnings.filterwarnings("ignore")
# Set random seed
np.random.seed(42)
# Number of samples
num_samples = 15
# Store the sampled quantum states
states = []
for i in range(num_samples):
# Create a single qubit circuit
cir = Circuit(1)
# Generate random rotation angles
phi, theta, omega = 2 * np.pi * np.random.uniform(size=3)
# Quantum gate operation
cir.rz(0, param=phi)
cir.ry(0, param=theta)
cir.rz(0, param=omega)
# Run the circuit
state = cir()
# Store the sampled quantum states
states.append(state.data)
# Call the Bloch sphere display function, enter the state parameter, and display the vector.
plot_state_in_bloch_sphere(states, show_arrow=True)
As shown in the figure above, we randomly sampled 15 times to generate 15 random single qubit quantum states. Display these 15 quantum states on the Bloch sphere respectively.
The description of Bloch sphere in the Paddle Quantum has rich functions, which can provide Bloch sphere display at different angles and different viewing distances. It also supports the storage of dynamic GIF graph, which is convenient for scholars to understand and learn.
For calling richer Bloch sphere functions, please refer to API of the function visual.plot_state_in_bloch_sphere().
Example: how to characterize the "trajectory" of the rotation of a single qubit quantum state on the Bloch sphere?¶
We know that the unitary operator of a single qubit can actually be regarded as rotating a Bloch vector on the Bloch sphere. The initial state of the quantum circuit corresponds to the initial Bloch vector on the Bloch sphere, and the final state of the quantum circuit corresponds to the Bloch vector after the rotation on the Bloch sphere.
Suppose we take the state from the $|0\rangle$ state through the $R_y(\frac{\pi}{4})$ revolving gate and the $R_z(\frac{\pi}{2})$ revolving gate as the initial state of the quantum state. Take the $U3(\theta = \frac{\pi}{2}, \phi = \frac{7\pi}{8}, \lambda = 2\pi)$ revolving gate as the unitary operator to be done. How to use Bloch sphere to clearly describe the process of unitary operator operation?
In Paddle Quantum, we use the function in visual package by entering init_state and $U3$ revolving gate to achieve this effect.
The specific codes are as follows:
# Create a single qubit circuit
cir = Circuit(1)
# Set the initial state of the quantum state
cir.ry(0, param=np.pi/4)
cir.rz(0, param=np.pi/2)
init_state = cir()
# Unitary operator operation to be performed
theta = np.pi/2
phi = 7*np.pi/8
lam = 2*np.pi
rotating_angle = [theta, phi, lam]
# Call Bloch sphere display function,input init_state,rotating_angle
plot_rotation_in_bloch_sphere(init_state, rotating_angle)
As shown in the figure above, on the right is the Bloch vector corresponding to the initial quantum state, and on the left is the Bloch vector corresponding to the quantum state after the unitary operator is completed. Red dots in the middle is the "trajectory" of the quantum state in the process of unitary operator.
The description of "trajectory" of Bloch sphere in Paddle Quantum also has rich functions, which can provide Bloch sphere display at different angles and different viewing distances. It also supports the storage of dynamic GIF graph, which is convenient for scholars to understand and learn.
For calling richer Bloch sphere functions, please refer to API of the function visual.plot_rotation_in_bloch_sphere().
What is a quantum logic gate?¶
In classical computers, we can apply basic logical operations (NOT gates, NAND gates, XOR gates, AND gates, and OR gates) on classical bits and combine them into more complicated operations. Quantum computing has a completely different set of logical operations, which are called quantum gates. We cannot compile existing C++ programs on a quantum computer. Because classical computers and quantum computers have different logic gate structures, quantum algorithms need to be constructed using quantum gates. Mathematically, a quantum gates can be expressed as a unitary matrix. Unitary operations could preserve vector length, which is a desirable property. Otherwise, if we operate on a pure state, it will be degraded into a mixed state, making it unreliable for the following running time. The unitary matrix is defined as:
$$ U^{\dagger}U = UU^{\dagger} = I, \quad \text{and} \quad \Vert |\psi\rangle \Vert = \Vert U|\psi\rangle\Vert = 1. \tag{6} $$where $U^{\dagger}$ is the conjugate transpose of $U$, and $I$ represents the identity matrix. But what is the physical meaning of representing quantum gates as unitary matrices? This implies that all quantum gates must be reversible. For any gate logic $U$, one can always find the corresponding reverse operation $U^\dagger$. In addition, the unitary matrix must be a square matrix, because the input and output of the quantum operation require the same number of qubits. A quantum gate acting on $n$ qubits can be written as a $2^n \times 2^n$ unitary matrix. The most common quantum gates act on one or two qubits, just like classical logic gates.
Single-qubit gate¶
Next, we introduce single-qubit gates in quantum computing, including the Pauli matrices $\{X, Y, Z\}$, single-bit rotation gates $\{R_x, R_y, R_z\}$ and the Hadamard gate $H$. Firstly, NOT gate is important for both classical and quantum computing,
$$ X := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix}. \tag{7} $$This quantum gate (unitary matrix) acts on the state of a single qubit (a complex vector). The operation is essentially multiplication between a matrix and a column vector:
$$ X |0\rangle := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} \begin{bmatrix} 1 \\0 \end{bmatrix} =\begin{bmatrix} 0 \\1 \end{bmatrix} = |1\rangle, \quad \text{and} \quad X |1\rangle := \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} \begin{bmatrix} 0 \\1 \end{bmatrix} =\begin{bmatrix} 1 \\0 \end{bmatrix}=|0\rangle. \tag{8} $$Recall the Bloch sphere representation, this operation $X$ acting on a qubit state (a point on the Bloch sphere) is equivalent to a rotation about the $x$ axis in the Bloch sphere with angle $\pi$ . This is why $X$ can be expressed as $R_x(\pi)$ (differ by a global phase $e^{-i\pi/2} = -i$ ). The other two Pauli matrices $Y$ and $Z$ are very similar in this sense (representing rotation around the $y$ and $z$ axes with angle $\pi$):
$$ Y := \begin{bmatrix} 0 &-i \\ i &0 \end{bmatrix}, \quad \text{and} \quad Z := \begin{bmatrix} 1 &0 \\ 0 &-1 \end{bmatrix}. \tag{9} $$Generally speaking, any quantum gate that rotates $\theta$ on the corresponding axis on the Bloch sphere can be expressed as
$$ R_x(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-i\sin \frac{\theta}{2} \\ -i\sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_y(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_z(\theta) := \begin{bmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{bmatrix}. \tag{10} $$In addition to the rotation gates, the most important single-qubit gate is the Hadamard gate. The corresponding Bloch spherical interpretation consists of two separate rotations, first rotating $\pi$ around the $z$-axis, and then rotating $\pi/2$ around the $y$-axis. Its matrix representation is
$$ H := \frac{1}{\sqrt{2}}\begin{bmatrix} 1 &1 \\ 1 &-1 \end{bmatrix}. \tag{11} $$Two-bit quantum gate¶
We can expand the idea of single-qubit gates to multi-qubit. There are two ways to realize this expansion. The first is to apply single-qubit gates on selected qubits, while the other qubits are not operated. The figure below gives a concrete example:
![**Figure 2.** Circuit representation and interpretation of two-qubit logic operations. [[Image source]](https://en.wikipedia.org/wiki/Quantum_logic_gate) intro-fig-hadamard](./figures/intro-fig-hadamard.png)
The quantum gate acting on two-qubit system can be expressed as a $4\times4$ unitary matrix
$$ U = H \otimes I = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 &1 \\ 1 &-1 \end{bmatrix} \otimes \begin{bmatrix} 1 &0 \\ 0 &1 \end{bmatrix} = \frac{1}{\sqrt{2}} \, \begin{bmatrix} 1 &0 &1 &0 \\ 0 &1 &0 &1 \\ 1 &0 &-1 &0 \\ 0 &1 &0 &-1 \end{bmatrix}. \tag{12} $$Another way is to apply two-qubit gates directly. For example, $\text{CNOT}$ gate will make the state of one qubit affect another qubit state.
$$ \text{CNOT} := \begin{bmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1 \\ 0 &0 &1 &0 \end{bmatrix}. \tag{13} $$When $\text{CNOT}$ acts on the computational basis, we have
$$ \text{CNOT} |00\rangle = |00\rangle, \quad \text{CNOT} |01\rangle = |01\rangle, \quad \text{CNOT} |10\rangle = |11\rangle, \quad \text{CNOT} |11\rangle = |10\rangle. \tag{14} $$We can conclude that when the first qubit is in the $|1\rangle$ state, $\text{CNOT}$ will act $X$ gate on the second qubit. If the first qubit is in the $|0\rangle$ state, then the second qubit is not affected in any way. This is why $\text{CNOT}$ stands for the controlled-$\text{NOT}$ gate. The following list contains frequently used quantum gates and their matrix representations. All of these quantum gates can be called in Paddle Quantum.
![**Figure 3.** List of common quantum gates. [[Image source]](https://en.wikipedia.org/wiki/Quantum_logic_gate) intro-fig-gates](./figures/intro-fig-gates.png)
Note: For more information, please see the following Wikipedia link.
What is measurement in quantum mechanics?¶
For a two-level quantum system, such as the spin of an electron, it can be spin up $\uparrow$ or spin down $\downarrow$, corresponding to state $|0\rangle$ and state $|1\rangle$. As mentioned before, the electron can be in a superposition state of spin up and down, which is $|\psi\rangle =\alpha |0\rangle + \beta |1\rangle$. The measurement will help us further understand what is a superposition state. It is worth noting that the measurement in quantum mechanics usually refers to a statistical result rather than a single measurement. This is due to the nature of measurements in quantum physics, which collapses the observed quantum state. For example, if we measure an electron in state $|\psi\rangle =\alpha |0\rangle + \beta |1\rangle$, we will have a probability of $|\alpha|^2$ to obtain the measurement results of spin up, and after measurement, the quantum state collapses to the post-measurement state $ |0\rangle$. Similarly, we also have a probability of $|\beta|^2$ to get the spin down post-measurement state $|1\rangle$. So if we want to get the value of $\alpha$ accurately, one experiment is obviously not enough. We need to prepare a lot of electrons in the superposition state $\alpha |0\rangle + \beta |1\rangle$, measure the spin of each electron, and then count the frequency. Measurement has a special place in quantum mechanics. If the reader finds it difficult to understand, we refer to Measurement in Quantum Mechanics for more information.
Example and exercise¶
Example: Using Paddle Quantum to create a $X$ gate¶
Note: All single-bit rotation gates are established as follows:
$$ R_x(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-i\sin \frac{\theta}{2} \\ -i\sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_y(\theta) := \begin{bmatrix} \cos \frac{\theta}{2} &-\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} ,\quad R_z(\theta) := \begin{bmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{bmatrix}. \tag{15} $$Therefore, it is not difficult to see that the $X$ gate can be expressed as $R_x(\pi)$. The following code will generate the $X$ gate:
# Set the angle parameter theta = pi
theta = np.pi
# Set the number of qubits required for calculation
num_qubits = 1
# Initialize the single-bit quantum circuit
cir = Circuit(num_qubits)
# Apply an Rx rotation gate to the first qubit (q0), the angle is pi
cir.rx(0, param=theta)
# Convert to numpy.ndarray
# Print out this quantum gate
print('The matrix representation of quantum gate is:')
print(cir.unitary_matrix().numpy())
The matrix representation of quantum gate is: [[-4.371139e-08+0.j 0.000000e+00-1.j] [ 0.000000e+00-1.j -4.371139e-08+0.j]]
There is a global phase $-i$ in front between the output and the $X$ (NOT) gate:
$$ \text{output} = \begin{bmatrix} 0 &-i \\ -i &0 \end{bmatrix} = -i\begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} = -i X. \tag{16} $$Can you figure out why such a global phase is not important in quantum computing? And not important in what sense?
Exercise: Create a $Y$ gate¶
Similar to the $X$ gate, try to create a $Y$ gate by filling the following code.
theta = "your code"
num_qubits = 1
cir = Circuit("your code")
cir.ry("your code")
print(cir.unitary_matrix().numpy())
As mentioned before, we have a global phase $-i$ in front:
$$ \text{output} = \begin{bmatrix} 0 &-1 \\ 1 &0 \end{bmatrix} = -i\begin{bmatrix} 0 &-i \\ i &0 \end{bmatrix} = -i Y. \tag{17} $$Quantum Neural Network¶
After the preparations from the last section, we now have the necessary knowledge to have a taste on quantum machine learning (QML). In Paddle Quantum, we provide a bunch of QML algorithms, which use quantum circuits to replace classical neural networks to complete machine learning tasks.
In this section, we introduce how to construct a parameterized quantum circuit (PQC), which is also called Quantum neural network (QNN) or Ansatz. The quantum circuit parameters are adjustable (usually these parameters are the angles $\theta$ of rotation gates). As we have seen in the last section, using angle $\pi$ to create a $X$ gate is probably the simplest QNN.
Example: How to create a quantum neural network?¶
QNN can usually be expressed as a combination of single-qubit gates and two-qubit gates. One of the widely used circuit architectures is the hardware-efficient ansatz consists of $\{R_x, R_y, R_z, \text{CNOT}_{j,j+1} \}$. They are easy to implement on near-term devices (usually superconducting qubits) because $\text{CNOT}_{j,j+1} $ only works on adjacent qubits and hence mitigate the topological connectivity issues. The figure below gives us a concrete example:
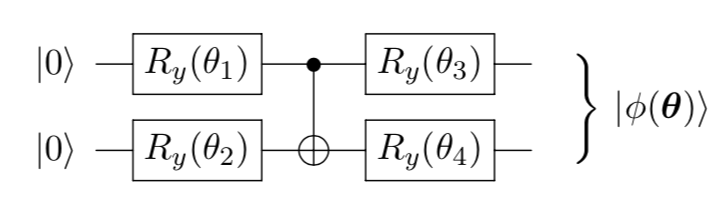
Each horizontal line here represents a qubit. We define the upper qubit to be the first qubit $q_0$; the lower one is the second qubit $q_1$. From left to right, it represents the order that we apply quantum gates. The leftmost quantum gate will be applied first. Next, let’s take a look on how to build this simple two-qubit quantum neural network on Paddle Quantum.
import numpy as np
import paddle
from paddle_quantum.ansatz import Circuit
# Set the angle parameter theta
theta = np.full([4], np.pi)
# Initialize the quantum circuit
num_qubits = 2
cir = Circuit(num_qubits)
# Add single-qubit rotation gates
cir.ry(0, param=theta[0])
cir.ry(1, param=theta[1])
# Add two-qubit gate
cir.cnot([0, 1])
# Add single-qubit rotation gates
cir.ry(0, param=theta[2])
cir.ry(1, param=theta[3])
print('The matrix representation of the quantum neural network U(theta=pi) in the figure is:')
print(cir.unitary_matrix().numpy().real)
The matrix representation of the quantum neural network U(theta=pi) in the figure is: [[-3.5527137e-15 -1.0000000e+00 -4.3711388e-08 4.3711395e-08] [-1.0000000e+00 -3.5527137e-15 4.3711381e-08 -4.3711388e-08] [ 4.3711388e-08 -4.3711395e-08 1.0000000e+00 -8.7422777e-08] [-4.3711381e-08 4.3711388e-08 8.7422777e-08 1.0000000e+00]]
Exercise¶
Given the following code, can you work out the corresponding circuit?
theta = np.full([6], np.pi)
num_qubits = 3
cir = Circuit(num_qubits)
cir.ry(0, param=theta[0])
cir.ry(1, param=theta[1])
cir.ry(2, param=theta[2])
cir.cnot([0, 1])
cir.cnot([1, 2])
cir.ry(0, param=theta[3])
cir.ry(1, param=theta[4])
cir.ry(2, param=theta[5])
Answer:
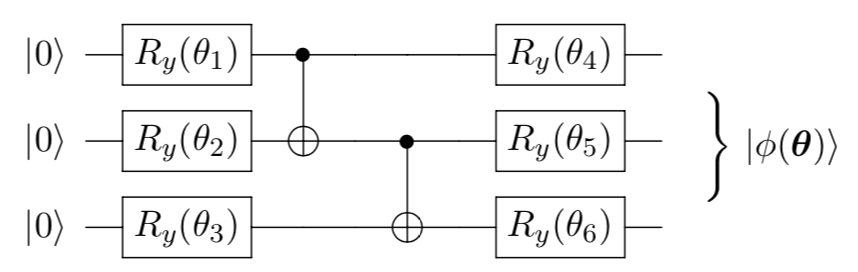
You can print your circuit using Paddle Quantum as follows:
print(cir)
--Ry(3.142)----*----Ry(3.142)---------------
|
--Ry(3.142)----x--------*--------Ry(3.142)--
|
--Ry(3.142)-------------x--------Ry(3.142)--
Built-in circuit templates¶
In the latest version of Paddle Quantum, we provide some built-in circuit templates to make users' life easier.
N = 3 # Set the number of qubits
# Initialize the quantum circuit
cir = Circuit(N)
# Apply Hadamard gate on each qubit
cir.superposition_layer()
# Prepare output state
# If the user does not enter the initial quantum state, the default initial is |00..0>
final_state = cir()
# Get the theoretical value of the probability distribution, set shots = 0
res = final_state.measure(shots = 0, plot = True)
N = 3 # Set the number of qubits
# Initialize the quantum circuit
cir = Circuit(N)
# Apply Ry(pi/4) rotation gate on each qubit
cir.weak_superposition_layer()
# Prepare output state
# If the user does not enter the initial quantum state, the default initial state is |00..0>
final_state = cir()
# Get the theoretical value of the probability distribution, set shots = 0
res = final_state.measure(shots = 0, plot = True)
The following figure depicts a handy circuit template complex_entangled_layer(DEPTH) . Users can extend the circuit architecture by changing the circuit depth parameter DEPTH. Define generalized rotation gate $U_3$ as
The $U_3$ rotation gate is equivalent to the combination of three different rotation gates:
$$ U_3(\theta, \phi, \varphi) = R_z(\phi)*R_y(\theta)*R_z(\varphi) := \begin{bmatrix} e^{-i\frac{\phi}{2}} & 0 \\ 0 & e^{i\frac{\phi}{2}} \end{bmatrix} \begin{bmatrix} \cos \frac{\theta}{2} &-\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} &\cos \frac{\theta}{2} \end{bmatrix} \begin{bmatrix} e^{-i\frac{\varphi}{2}} & 0 \\ 0 & e^{i\frac{\varphi}{2}} \end{bmatrix}. \tag{20} $$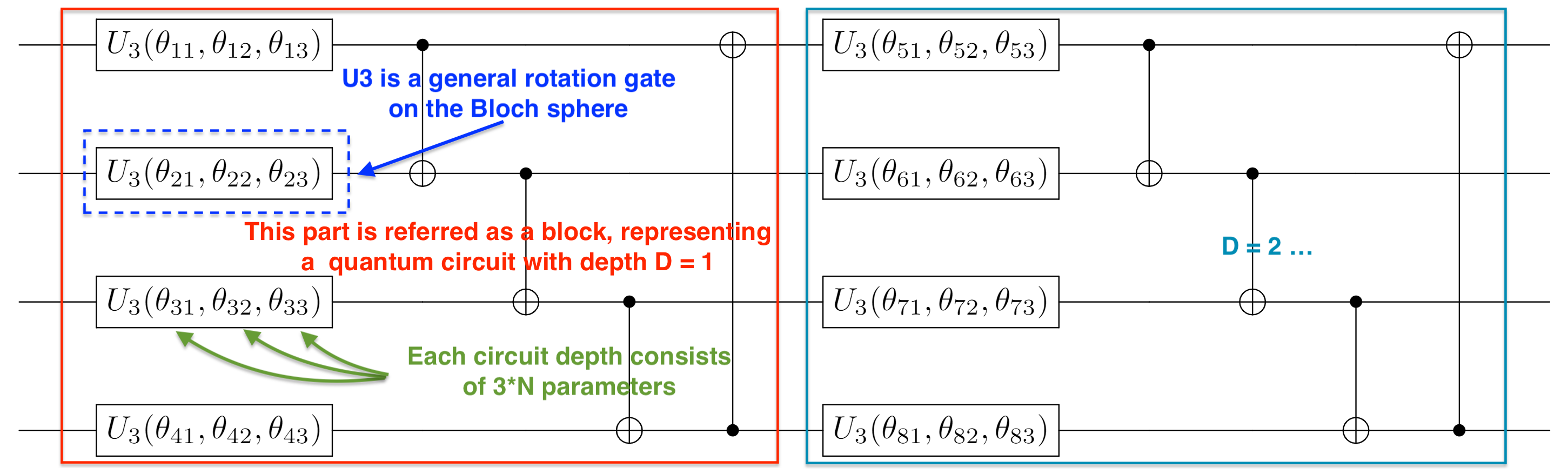
When our task does not involve imaginary numbers, it is more efficient to use the circuit template real_entangled_layer(DEPTH) ($R_y$ instead of $U_3$).
N = 4 # Set the number of qubits
DEPTH = 6 # Set the quantum circuit depth
paddle.seed(1)
# Initialize the quantum circuit
cir = Circuit(N)
# Add a complex strong entanglement structure QNN with depth D = 6 {Rz+Ry+Rz/U3 + CNOT's}
cir.complex_entangled_layer(depth=DEPTH)
# Prepare output state
# If the user does not enter the initial quantum state, the default initial is |00..0>
final_state = cir.forward()
# Measure the output state [0, 1, 2] qubits 2048 times, and count the frequency of the measurement results
res = final_state.measure(shots = 2048, qubits_idx = [0, 1, 2], plot = True)
An Introduction to Variational Quantum Algorithm¶
Overview¶
Many classical problems, such as travelling salesman problem, classification, finding the ground state of a molecular, can all be regarded as optimization problems. Limited to the classical computer capabilities, such problems are extremely difficult to be solved.
The development of the quantum computers provides another approach to deal with these problems. It is quite believed that in the next few years, Noisy Intermediate-Scale Quantum (NISQ) devices with tens or hundreds of qubits will be developed and used for real-world experiments.
Paddle Quantum provides a bunch of high-level quantum algorithms. We believe from these tutorials you will learn more about quantum information and feel the potential of the quantum computers.
To make it easy to understand, we provide one simple example here, preparing pure quantum state. With this example, we introduce the basic idea and the program structure how to realize Variational Quantum Algorithms (VQA), i.e. using quantum neural networks (QNN) to solve optimization problems., which will help you understand tutorials easier.
Note: The different operating modes of Paddle Quantum for the pure states and the mixed states and the more detailed introduction to PaddlePaddle will be given in the next two sections.
Use Quantum Neural Networks to Solve Optimization Problems¶
QNN is a quantum algorithm used for solving optimization problems. It generalizes the idea of the classical neural networks (CNN) to the quantum region.
To help you understand QNN, here we first introduce the basic concept in optimization problem and CNN.
CNN and the optimization problems¶
CNN is a classical algorithm, which use neural networks to optimize some loss function.The neural network can be characterized by its structure, the weights $\vec{w}$ and the bias $\vec{b}$ in it.
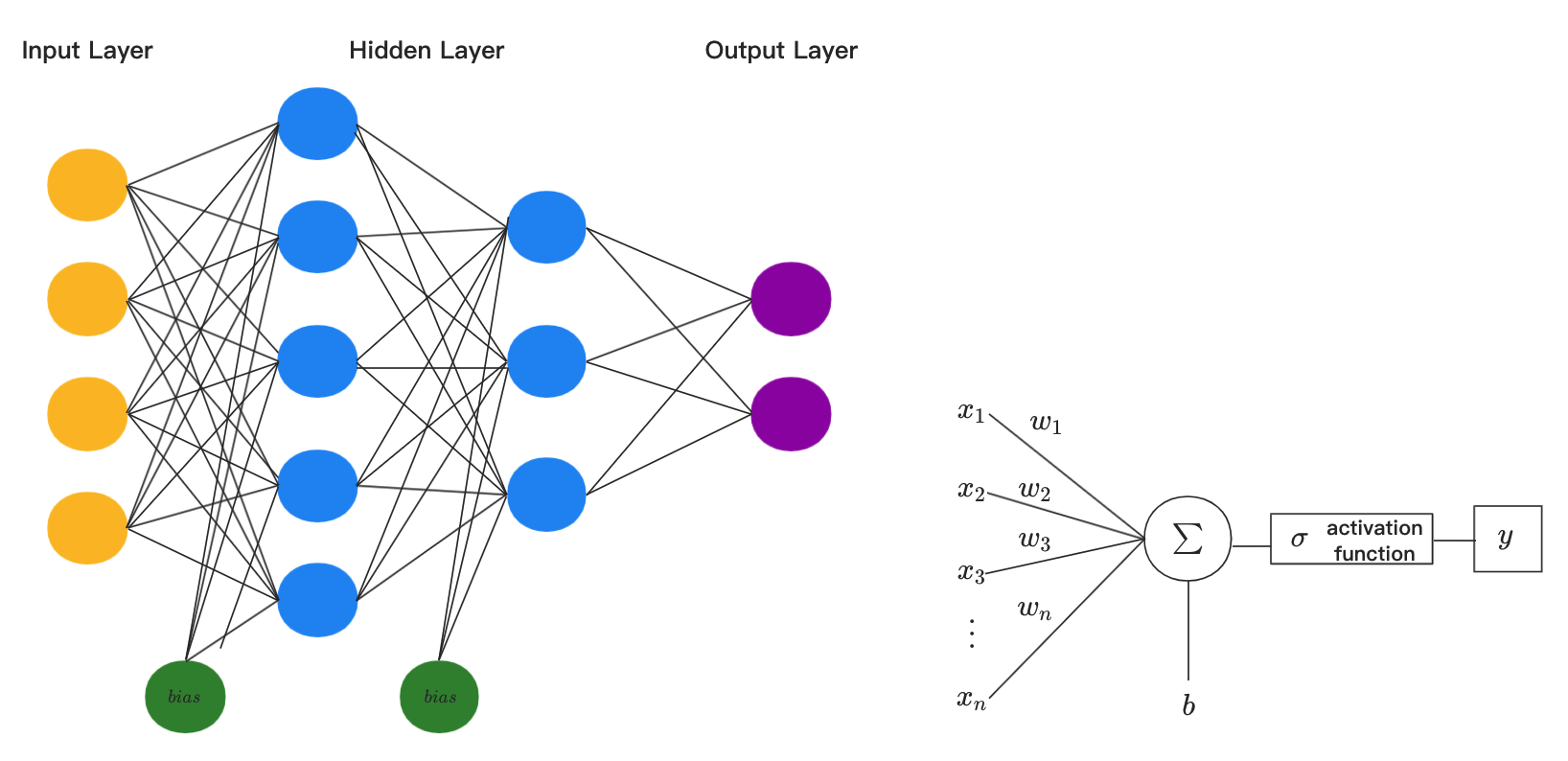
Mathematically, use CNN to solve an optimization problem can be regarded as follows: Modify the variables $\vec{w}$, $\vec{b}$ in the neural network, to get the best output vector $\hat{y}(\vec{w},\vec{b})$, which minimize a loss function $L(\hat{y}(\vec{w},\vec{b}))$
In the salesman problem, the loss function can be the distance salesman travels. In classification, the loss function can be how real output labels different from the target ones.
Use QNN to solve the optimization problems¶
The difference between QNN and CNN is that QNN use quantum states and quantum gates to build the neural networks (a quantum circuit).
A QNN can also be characterized by its structure, how you connect your gates, and a set of parameters $\vec{\theta}$, which describes which gate you put in the circuit.
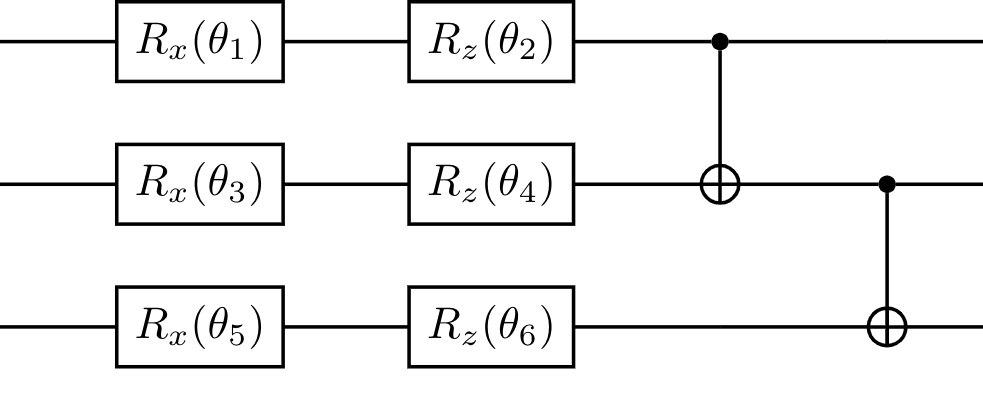
Here is a very simple example of a quantum neural network, with 3 qubits and 1 layer. $R_x(\theta_1)$ means performing a rotation around $x$-axis with angle $\theta_1$. Here $\{\theta_1,\cdots,\theta_6\}$ are variables.
- Note 1: arbitrary gate can be decomposed into one-qubit gates and two-qubit gates (e.g., CNOT).
- Note 2: one-qubit gates can be characterized by its rotating axis and its rotating angles $\theta$.
With these ideas in mind, you can see that by modifying the parameter $\theta$ in this circuit, and when the depth (the number of layers) of the circuit is large, we can generate arbitrary unitary gate with this circuit.
Mathematically, VQA (use QNN to solve optimization problem) can be regarded as follows: Modify the variables $\theta$ in a (given structure) quantum circuit to get the best output state $\rho(\vec{\theta})$, which minimize a loss function $L(\rho(\vec{\theta}))$. The input state is usually chosen to be $|00\cdots0\rangle$.
In the following, we will use a very simple example to see how to do this optimization with Paddle Quantum.
Use Paddle Quantum to Realize QNN: A Simple Example¶
The task we consider here is very simple: use VQA to prepare a pure state. This task is simple but still important as when the pure state is large and highly entangled, how to get the unitary gate to create this state will be difficult. QNN provides a method to use single-qubit gates and two-qubit gates to realize this task.
For simplicity, here the target state we want to create is $|01\rangle\otimes|+\rangle$. Readers could modify the following code to try to create entangled state with larger qubits number.
The Structure of Using QNN¶
Use QNN to solve an optimization problem usually contains three steps
Step 1: Create your own quantum circuit as a function¶
- step 1.1: Create an N qubit circuit
- step 1.2: Add gates to each layer
# import packages
import paddle
import numpy as np
from paddle_quantum.ansatz import Circuit
from paddle_quantum.state import State
import matplotlib.pyplot as plt
def circuit(N, DEPTH):
"""
Input data:
N, qubits number
DEPTH, layers number
Return:
cir, the final circuit
"""
# step 1.1: Create an N qubit circuit
cir = Circuit(N)
# step 1.2: Add gates to each layer
for dep in range(DEPTH):
for n in range(N):
cir.rx(n) # add an Rx gate to the n-th qubit
cir.rz(n) # add an Rz gate to the n-th qubit
for n in range(N-1):
cir.cnot([n, n + 1]) # add CNOT gate to every neighbor pair
return cir
Here is the figure of the circuit we use, which has 3 qubits, and 2 layers, $\theta$ is randomly generated:
N = 3
DEPTH = 2
cir = circuit(N, DEPTH)
print(cir)
--Rx(-1.26)----Rz(1.092)----*----Rx(2.778)----Rz(1.194)-----------------*-------
| |
--Rx(0.219)----Rz(0.882)----x--------*--------Rx(-1.00)----Rz(-1.58)----x----*--
| |
--Rx(0.774)----Rz(-0.53)-------------x--------Rx(-1.34)----Rz(-0.88)---------x--
Step 2: Define and calculate your loss function¶
Here we use “-fidelity” between the real output state and the target state to be the loss function. When the real output state is the target state, “-fidelity” will be “-1”, which is the minimum number.
def loss_func(cir: Circuit, psi: State) -> paddle.Tensor:
final_state = cir().data
psi_target = psi.data
inner = paddle.matmul(dagger(final_state), psi_target)
loss = -paddle.real(paddle.matmul(dagger(inner), inner))
return loss
Step 3: backward part, optimize the loss function over iterations¶
The optimizer we usually use is Adam.
# First, we give the parameters used for learning
ITR = 115 # iteration number
LR = 0.2 # learning rate
# The target state we want: as a row vector here
psi_vec = np.kron(np.kron(np.array([[1],[0]]), np.array([[0], [1]])), np.array([[1/np.sqrt(2)], [1/np.sqrt(2)]]))
# Instantiate the target state as a State
psi_target = State(paddle.to_tensor(psi_vec).cast('complex64'))
# Record the iteration:
loss_list = []
# Choose the optimizer, usually we use Adam
opt = paddle.optimizer.Adam(learning_rate = LR, parameters = cir.parameters())
# Optimize during iteration
for itr in range(ITR):
# Calculate the loss
loss = loss_func(cir, psi_target)
# Backward optimize via Gradient descent algorithm
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# Record the learning curve
loss_list.append(loss.numpy())
if itr % 10 == 0:
print('iter:', itr, ' loss: %.4f' % loss.numpy())
iter: 0 loss: -0.0430 iter: 10 loss: -0.8984 iter: 20 loss: -0.9637 iter: 30 loss: -0.9835 iter: 40 loss: -0.9944 iter: 50 loss: -0.9975 iter: 60 loss: -0.9994 iter: 70 loss: -0.9999 iter: 80 loss: -0.9999 iter: 90 loss: -1.0000 iter: 100 loss: -1.0000 iter: 110 loss: -1.0000
Step 4: Now we have finished our calculation, let’s see the results¶
# Print the output
print('The minimum of the loss function: ', loss_list[-1])
# The parameters after optimization
theta_final = [param.numpy() for param in cir.parameters()]
print("Parameters after optimizationL theta:\n", theta_final, "\n")
# Draw the circuit picture and the output state
print(cir)
The minimum of the loss function: [-0.99999565]
Parameters after optimizationL theta:
[array([[-3.1392097]], dtype=float32), array([[3.3646517]], dtype=float32), array([[8.64552e-05]], dtype=float32), array([[-0.05600645]], dtype=float32), array([[1.7714778]], dtype=float32), array([[1.1910632]], dtype=float32), array([[3.141264]], dtype=float32), array([[-1.0635952]], dtype=float32), array([[-0.00058735]], dtype=float32), array([[-1.9210217]], dtype=float32), array([[-0.49833927]], dtype=float32), array([[-0.42850757]], dtype=float32)]
--Rx(-3.13)----Rz(3.365)----*----Rx(3.141)----Rz(-1.06)-----------------*-------
| |
--Rx(0.000)----Rz(-0.05)----x--------*--------Rx(-0.00)----Rz(-1.92)----x----*--
| |
--Rx(1.771)----Rz(1.191)-------------x--------Rx(-0.49)----Rz(-0.42)---------x--
# Print the final state
state_final = cir()
print("state_final:\n", state_final.data.numpy())
# Print the loss function during iteration
plt.figure(1)
ITR_list = []
for i in range(ITR):
ITR_list.append(i)
func = plt.plot(ITR_list, loss_list, alpha=0.7, marker='', linestyle='-', color='r')
plt.xlabel('iterations')
plt.ylabel('loss')
plt.legend(labels=["loss function during iteration"], loc='best')
plt.show()
state_final: [-9.4619114e-05-1.5272114e-04j -7.3144663e-05-1.6564086e-04j 5.2861774e-01+4.6885246e-01j 5.2879083e-01+4.7023308e-01j 3.8210783e-05+1.0977582e-04j 3.8404934e-05+1.0973777e-04j -6.7721255e-04+5.0217507e-04j -8.2200416e-04-1.8180218e-04j]
As the “-Fidelity” becomes “-1”, this circuit learns to prepare the target state “$|01\rangle\otimes|+\rangle$".
Practice¶
- Try to prepare entangled states.
- Try to prepare larger quantum states with larger qubits number 'N'.
- Change circuit layer number, ‘DEPTH’, and see how the performance change
- Change the learning rate 'LR'.
Operating Mode of Paddle Quantum¶
Wave function vector mode¶
The so-called wave function mode is to use complex vectors to represent and store the quantum states. Vector mode can only handle pure states, but this mode efficiently supports 20+ qubit operations on personal computer hardware. Users can test the limits of their computers. Under this representation, the essential operation of the quantum gate (unitary matrix) acting on qubits (a complex vector to describe the state) is multiplying a matrix by a vector:
$$ |\psi\rangle = U |\psi_0\rangle. \tag{21} $$Calling the function paddle_quantum.set_backend("state_vector") changes the mode to state vector mode. Note that the operating model is the state vector mode by default. One need to call the function final_state = cir(input_state=initial_state) to run a circuit cir, where the input state is initial state and the output state is final_state, both of which are state vectors. If we don't enter any input state, it will be set into the $\lvert {0}\rangle$ state by default. Let's take a specific example:
import paddle_quantum
from paddle_quantum.ansatz import Circuit
from paddle_quantum.state import zero_state, random_state
N = 10 # Set the number of qubits
DEPTH = 6 # Set the quantum circuit depth
# Set state vector mode
paddle_quantum.set_backend("state_vector")
# Call the built-in zero state function to create a zero state
initial_state1 = zero_state(num_qubits=N)
# Call the built-in random state function to create a random state
initial_state2 = random_state(num_qubits=N)
# Initialize the quantum circuit
cir = Circuit(N)
# Add a real entanglement structure QNN {Ry+CNOT's} with depth of DEPTH
cir.real_entangled_layer(depth=DEPTH)
# Run the circuit on the initial state, If the user does not enter the initial quantum state, the default initial state is |00..0>
final_state1 = cir(initial_state1)
print(final_state1.data.numpy())
[-5.4838351e-04+0.j -2.7753570e-04+0.j 6.3722655e-05+0.j ... -2.3885426e-04+0.j 1.8981205e-04+0.j -6.4218853e-05+0.j]
Density matrix mode¶
Paddle Quantum also supports the density matrix mode, which is to use density matrices $\rho = \sum_i P_i |\psi_i\rangle\langle\psi_i|$ to represent and store quantum states. This mode can supports mixed state simulation . But in density matrix mode, personal computer hardware can only support around 10 qubits. Please pay attention to this limitation. We are constantly optimizing the performance of the simulator in this mode. Under this representation, quantum gates (unitary matrices) acting on the quantum states (Hermitian matrix with a trace of 1) can be viewed as matrix multiplication:
$$ \rho = U \rho_0 U^\dagger. \tag{22} $$One need to call the function paddle_quantum.set_backend("density_matrix") to set the density matrix mode. The way of running a circuit is almost the same as in the state vector mode, except that both of input and output states are density matrices. Here is an example:
import paddle_quantum
from paddle_quantum.ansatz import Circuit
from paddle_quantum.state import zero_state, random_state, completely_mixed_computational
N = 2 # Set the number of qubits
DEPTH = 6 # Set the quantum circuit depth
# Set density matrix mode
paddle_quantum.set_backend("density_matrix")
# Call the built-in |00..0><00..0| initial state
initial_state1 = zero_state(N)
# Call the built-in random quantum state, you can specify whether to allow complex number elements and matrix rank
initial_state2 = random_state(N, is_real=False, rank=4)
# Call the complete mixed state under the built-in calculation base
initial_state3 = completely_mixed_computational(N)
# Initialize the quantum circuit
cir = Circuit(N)
# Add a real number strong entanglement structure QNN {Ry+CNOT's} with depth of DEPTH
cir.real_entangled_layer(depth=DEPTH)
# Prepare output state
# If the user does not enter the initial quantum state, the default initial is |00..0><00..0|
final_state = cir(initial_state2)
print(final_state.data.numpy())
[[ 0.5808575 -1.0710210e-08j -0.07621858-1.5724729e-01j 0.3288467 +5.1938809e-02j 0.24451724-1.8499317e-03j] [-0.07621857+1.5724732e-01j 0.08419196-5.5879354e-09j -0.05945612+7.4587353e-02j -0.01910382+7.2627157e-02j] [ 0.32884675-5.1938821e-02j -0.05945611-7.4587345e-02j 0.2059458 +1.1175871e-08j 0.12963158-5.9516393e-03j] [ 0.24451725+1.8499183e-03j -0.01910383-7.2627142e-02j 0.12963158+5.9516374e-03j 0.12900479-5.1804818e-09j]]
Exercise: How to prepare Bell states from computational basis¶
Bell state is a widely used quantum entangled state, which can be expressed as
$$ |\Phi^+\rangle = \frac{1}{\sqrt{2}} \big(|00\rangle + |11\rangle\big) = \frac{1}{\sqrt{2}} \, \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix}. \tag{23} $$So how do we use Paddle Quantum to prepare a Bell state? We can use the following quantum circuit :

# Set state vector mode
paddle_quantum.set_backend("state_vector")
# Create a circuit
cir = Circuit(2)
# Add quantum gates
cir.h(0)
cir.cnot([0, 1])
# If the user does not enter the initial quantum state, the default initial is |00..0>
output_state = cir()
# We measure the output state 2048 times and obtain the frequency distribution of the measurement results
output_state.measure(shots = 2048, plot = True)
print('The Bell state is:\n', output_state.data.numpy())
The Bell state is: [0.70710677+0.j 0. +0.j 0. +0.j 0.70710677+0.j]
PaddlePaddle Optimizer Tutorial¶
Example: Using gradient descent in PaddlePaddle to optimize multivariable functions¶
In this section, we will learn how to use an optimizer in PaddlePaddle to find the minimum value of a multivariable function, for example,
$$ \mathcal{L}(\theta_1, \theta_2, \theta_3) = (\theta_1)^2 + (\theta_2)^2 + (\theta_3)^2 + 10. \tag{24} $$It is clear when $\theta_1 = \theta_2 = \theta_3 = 0$, $\mathcal{L}$ takes the minimum value of 10.
# Set hyper parameter
theta_size = 3
ITR = 200 # Set the number of iterations
LR = 0.5 # Set the learning rate
SEED = 1 # Fix random number seed
paddle.seed(SEED)
class Optimization_ex1(paddle.nn.Layer):
def __init__(self, shape, dtype='float32'):
super(Optimization_ex1, self).__init__()
# Initialize a list of learnable parameters with length theta_size
# Use the uniform distribution of [-5, 5] to fill the initial value
self.theta = self.create_parameter(shape=shape,
default_initializer=paddle.nn.initializer.Uniform(low=-5., high=5.),
dtype=dtype, is_bias=False)
# Define loss function and forward propagation mechanism
def forward(self):
loss = self.theta[0] ** 2 + self.theta[1] ** 2 + self.theta[2] ** 2 + 10
return loss
# Record intermediate optimization results
loss_list = []
parameter_list = []
# Define network dimensions
myLayer = Optimization_ex1([theta_size])
# Use Adam optimizer to get relatively good convergence
# Of course you can change to SGD or RMSprop.
opt = paddle.optimizer.Adam(
learning_rate = LR, parameters = myLayer.parameters())
# Iteration of optimization
for itr in range(ITR):
# Forward propagation calculates the loss function
loss = myLayer()[0]
# Backpropagation optimizes the loss function
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# Record the learning process
loss_list.append(loss.numpy()[0])
parameter_list.append(myLayer.parameters()[0].numpy())
print('The minimum value of the loss function is:', loss_list[-1])
The minimum value of the loss function is: 10.0
Exercise: Finding Eigenvalues¶
Next, let's try a more complicated loss function. First, we introduce a random Hermitian matrix $H$ whose eigenvalues are the diagonal elements of matrix $D$, where
$$ D = \begin{bmatrix} 0.2 &0 \\ 0 &0.8 \end{bmatrix}. \tag{25} $$Don't worry, we will help you generate this Hermitian matrix $H$.
Initialize the parameter vector $\boldsymbol{\theta}$ to construct a simple linear operation $U(\boldsymbol{\theta}) = R_z(\theta_1)*R_y(\theta_2)*R_z(\theta_3)$:
$$ U(\theta_1, \theta_2, \theta_3) = \begin{bmatrix} e^{-i\frac{\theta_1}{2}} & 0 \\ 0 & e^{i\frac{\theta_1}{2}} \end{bmatrix} \begin{bmatrix} \cos \frac{\theta_2}{2} &-\sin \frac{\theta_2}{2} \\ \sin \frac{\theta_2}{2} &\cos \frac{\theta_2}{2} \end{bmatrix} \begin{bmatrix} e^{-i\frac{\theta_3}{2}} & 0 \\ 0 & e^{i\frac{\theta_3}{2}} \end{bmatrix}. \tag{26} $$Multiply this matrix (ansatz) by $|0\rangle$ to get a new 2-dimensional complex vector
$$ |\phi\rangle = U(\theta_1, \theta_2, \theta_3)|0\rangle. \tag{27} $$Then, we define the loss function as
$$ \mathcal{L}(\theta_1, \theta_2, \theta_3) = \langle\phi| H |\phi\rangle = \langle0| U^{\dagger}H U |0\rangle. \tag{28} $$Let's see what we got after optimization!
from scipy.stats import unitary_group
# V is a 2x2 random unitary matrix
V = unitary_group.rvs(2)
# The diagonal elements in D are the eigenvalue of H
# You can change the diagonal element value here
D = np.diag([0.2, 0.8])
# V_dagger is the Hermitian transpose of V
V_dagger = V.conj().T
# @: Represents matrix multiplication
H = (V @ D @ V_dagger)
print('The randomly generated matrix H according to the spectral decomposition is:')
print(H,'\n')
print('The eigenvalues of H are:')
print(np.linalg.eigh(H)[0])
The randomly generated matrix H according to the spectral decomposition is: [[0.29312716+0.j 0.20572598-0.06986022j] [0.20572598+0.06986022j 0.70687284+0.j ]] The eigenvalues of H are: [0.2 0.8]
# Hyper parameter settings
theta_size = 3 # set theta dimension
num_qubits = 1 # Set the number of qubits
ITR = 50 # Set the number of iterations
LR = 0.5 # Set the learning rate
SEED = 1 # Fix random seed for initializing theta parameter
paddle.seed(SEED)
# Set the circuit module separately
def U_theta() -> Circuit:
# Initialize the circuit and add the quantum gates
cir = Circuit(num_qubits)
cir.rz(0)
cir.ry(0)
cir.rz(0)
# Return circuit
return cir
def loss_func(cir: Circuit, H: paddle.Tensor) -> paddle.Tensor:
# Get the unitary matrix representation of the quantum neural network
U = cir.unitary_matrix().cast('complex64')
# Conjugate transpose operation
U_dagger = dagger(U)
# Calculate the loss function
loss = paddle.real(matmul(U_dagger, matmul(H, U)))[0][0]
return loss
loss_list = []
parameter_list = []
cir = U_theta()
# SGD optimizer
opt = paddle.optimizer.SGD(learning_rate = LR, parameters = cir.parameters())
# Optimization cycle
for itr in range(ITR):
# Forward propagation calculates loss function
loss = loss_func(cir, paddle.to_tensor(H).cast('complex64'))
# Back propagation minimizes the loss function
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# Record the learning curve
loss_list.append(loss.numpy()[0])
parameter_list.append(myLayer.parameters()[0].numpy())
if itr % 5 == 0:
print('iter:', itr, 'loss: %.4f'% loss.numpy())
print('The minimum value of the loss function is:', loss_list[-1])
iter: 0 loss: 0.2134 iter: 5 loss: 0.2055 iter: 10 loss: 0.2024 iter: 15 loss: 0.2011 iter: 20 loss: 0.2005 iter: 25 loss: 0.2002 iter: 30 loss: 0.2001 iter: 35 loss: 0.2000 iter: 40 loss: 0.2000 iter: 45 loss: 0.2000 The minimum value of the loss function is: 0.20000416
We can change the eigenvalues of $H$. If the diagonal matrix after diagonalization is changed to
$$ D = \begin{bmatrix} 0.8 &0 \\ 0 &1.2 \end{bmatrix}. \tag{29} $$We still get the minimum eigenvalue of $\lambda_{\text{min}}(H)=0.8$. Can you find the reason behind it? Or is there any theory behind this?
References¶
[1] Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information. (Cambridge university press, 2010).
[2] Phillip Kaye, Laflamme, R. & Mosca, M. An Introduction to Quantum Computing. (2007).
[3] Biamonte, J. et al. Quantum machine learning. Nature 549, 195–202 (2017).
[4] Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 56, 172–185 (2015).
[5] Benedetti, M., Lloyd, E., Sack, S. & Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 4, 043001 (2019).