Entanglement Distillation -- Protocol Design with LOCCNet

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview

Quantum entanglement plays a vital role in quantum communication, quantum computing, and many other quantum technologies. Therefore, detecting, transmitting, and distributing quantum entanglement reliably are essential tasks if we want to build real applications in those fields. However, errors are inevitable in the real world. They could come from imperfect equipment when we create entanglement (preparation errors), or the quantum channel used to transmit entanglement is noisy, and we gradually lose the degree of entanglement as the transmission distance increases. The aim of entanglement distillation is to compensate for those losses and restore a maximally entangled state at the cost of many noisy entangled states. In this sense, one could also refer entanglement distillation as a purification/error-correction protocol. This process often involves two remote parties Alice and Bob such that only Local Operations and Classical Communication (LOCC) are allowed [1]. Many distillation protocols have been proposed since 1996, including the famous BBPSSW [2] and the DEJMPS protocol [3].

However, the BBPSSW and DEJMPS distillation protocols are designed for specific types of noisy states (i.e., isotropic states and Bell-diagonal states, respectively). It is nearly impossible to find a single distillation protocol that could purify all kinds of noises. Due to the complicated mathematical structure of LOCC, designing a new distillation protocol is time-consuming with paper and pencil only. LOCCNet, a machine learning framework for LOCC protocols, is designed to reduce the effort as much as possible. With LOCCNet, it will be easier to design new distillation protocols as long as we can characterize the mathematical form of noise introduced to the entanglement resources.

Preliminary

In the context of entanglement distillation, we usually use the state fidelity $F$ between the distilled state $\rho_{out}$ and the maximally entangled Bell state $|\Phi^+\rangle$ to quantify the performance of a distillation protocol, where

$$ F(\rho_{out}, \Phi^+) \equiv \langle \Phi^+|\rho_{out}|\Phi^+\rangle. \tag{1} $$

Note: In general, LOCC distillation protocols are probabilistic, and hence we are also interested in the success rate $p_{succ}$.

Protocol design logic

In this tutorial, we will go through an example that distills four identical isotropic states (or Werner state) $\rho_{in}= \rho_{\text{iso}}$ into a single final state $\rho_{out}$ with a higher state fidelity $F$ (closer to the Bell state $|\Phi^+\rangle$). We call this type of protocol as the $4\rightarrow 1$ LOCC distillation class, while the original BBPSSW and DEJMPS protocols belong to the $2\rightarrow 1$ LOCC distillation class. The isotropic state is a parametrized family of mixed states consist of $|\Phi^+\rangle$ and the completely mixed state (white noise) $I/4$,

$$ \rho_{\text{iso}}(p) = p\lvert\Phi^+\rangle \langle\Phi^+\rvert + (1-p)\frac{I}{4}, \quad p \in [0,1] \tag{2} $$

In our example, we set $p=0.7$ and the input state becomes:

$$ \rho_{in} = \rho_{\text{iso}}(0.7)= 0.7\lvert\Phi^+\rangle \langle\Phi^+\rvert + 0.075 I. \tag{3} $$

To fulfill the task of distillation through LOCC, we introduce two remote parties, $A$ (Alice) and $B$ (Bob). At the very beginning, they share four copies of entangled qubit pairs $\rho_{A_0B_0}, \rho_{A_1B_1}, \rho_{A_2B_2}$ and $\rho_{A_3B_3}$. Each copy is initialized as $\rho_{in} = \rho_{\text{iso}}(p =0.7)$. Alice holds four qubits $A_0, A_1, A_2, A_3$ in one place and Bob holds $B_0, B_1, B_2, B_3$ in another place. With these initial setups, Alice and Bob could choose the communication rounds $r$, which indicates how many times they would measure their subsystems and transmit classical data with each other. For simplicity, it is natural to start with $r=1$. Then, Alice and Bob can use LOCCNet to find out the correct local operations (encoded as quantum neural networks, QNNs) before communication by following the steps below:

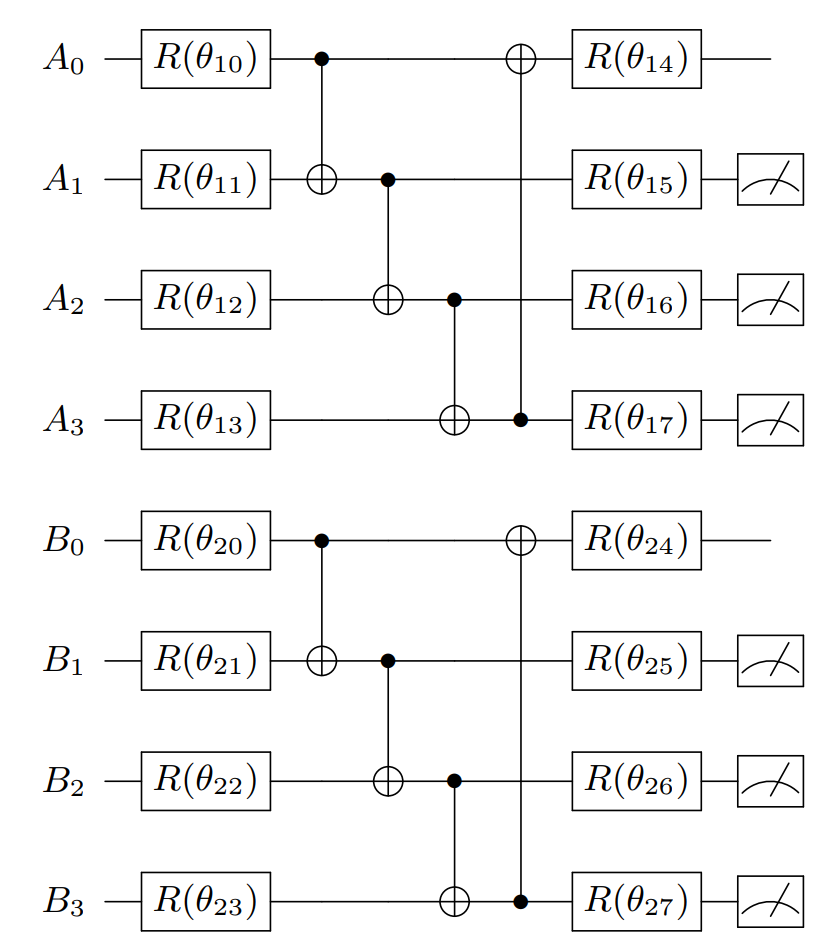
1. Design a general QNN architecture $U(\boldsymbol\theta)$ as shown in Figure 1, where each $R(\theta)$ represents a general rotation operation on the Bloch sphere. They are referred as the u3(theta, phi, lam, which_qubit) gate in Paddle Quantum.
2. After implementing the QNN, Alice and Bob measure all of the qubits except $A_0$ and $B_0$ in the computational basis. Then the measurement results $M = \{m_{A_1}m_{B_1}, m_{A_2}m_{B_2}, m_{A_3}m_{B_3}\}$ will be exchanged through a classical channel.
3. If the measurement results of all qubit pairs are the same (each pair $m_{A_1}m_{B_1}, m_{A_2}m_{B_2}, m_{A_3}m_{B_3}$ is either 00 or 11), the distillation is successful, and the pair $A_0B_0$ is reserved as the memory qubit pair to store the purified entanglement; If the measurement results are different, the protocol fails. Discard the quantum pair $A_0B_0$. At this point, we obtain the purified quantum pair $A_0B_0$ probabilistically, and its state is denoted as $\rho_{AB}'$.
4. Define the accumulated loss function $L = \sum_{m_{A_j}m_{B_j}\in \{00,11\}} \big(1- \text{Tr}(\rho_{tar}\rho_{AB}')\big)$ over the successful distillations, where $\text{Tr}(\rho_{tar}\rho_{AB}')$ is the state overlap between the current state $\rho_{AB}'$ and the target state $\rho_{tar}=\lvert\Phi^+\rangle \langle \Phi^+\rvert$.
5. Use gradient-based optimization methods to update parameters in QNN and minimize the loss function.
6. Repeat steps 1-5 until the loss function converges.
7. Output the purified state $\rho_{out} = \rho'_{A_0B_0}$.

Note: The QNN structure used is merely an illustration. Readers are welcomed to try their own designs.

Figure 1: Schematic diagram of a distillation protocol designed with LOCCNet.

Simulation with Paddle Quantum

First, we import all the dependencies:

import numpy as np
import paddle
from paddle import matmul, trace
import paddle_quantum
from paddle_quantum.locc import LoccNet
from paddle_quantum.state import isotropic_state, bell_state
from paddle_quantum.qinfo import logarithmic_negativity
# Change to density matrix mode
paddle_quantum.set_backend('density_matrix')

Secondly, we define the QNN and the loss function:

class LOCC(LoccNet):
    def __init__(self):
        super(LOCC, self).__init__()

        # Add the first party Alice 
        # The first parameter 4 stands for how many qubits A holds
        # The second parameter records the name of this party
        self.add_new_party(4, party_name="Alice")
        # Add the second party Bob
        # The first parameter 4 stands for how many qubits B holds
        # The second parameter records the name of this party
        self.add_new_party(4, party_name="Bob")

        # Generate input isotropic states
        _state = isotropic_state(2, 0.7)
        # Distribute the pre-shared entangled states
        self.set_init_state(_state, [["Alice", 0], ["Bob", 0]])
        self.set_init_state(_state, [["Alice", 1], ["Bob", 1]])
        self.set_init_state(_state, [["Alice", 2], ["Bob", 2]])
        self.set_init_state(_state, [["Alice", 3], ["Bob", 3]])

        # Create Alice's circuit
        self.cir1 = self.create_ansatz("Alice")
        self.QNN(self.cir1)
        # Create Bob's circuit
        self.cir2 = self.create_ansatz("Bob")
        self.QNN(self.cir2)

    def QNN(self, cir):
        '''
        Define the QNN illustrated in Figure 1
        '''
        cir.u3('full')
        cir.cnot('cycle')
        cir.u3('full')

    def New_Protocol(self):
        status = self.init_status
        # Execute Alice's circuit
        status = self.cir1(status)
        # Execute Bob's circuit
        status = self.cir2(status)

        # Measure qubits，["000000", "000011","001100","110000","001111","111100","110011","111111"] represent successful cases
        status1 = self.measure(status, [["Alice", 1], ["Bob", 1],["Alice", 2], ["Bob", 2], ["Alice", 3], ["Bob", 3]], 
                               ["000000", "000011", "001100", "110000", "001111", "111100", "110011", "111111"])

        # Trace out all the qubits but A_0 and B_0
        status_fin = self.partial_state(status1, [["Alice", 0], ["Bob", 0]])
        target_state = bell_state(2)

        # Calculate loss function
        loss = 0
        for idx in range(0, len(status_fin)):
            loss += 1 - paddle.real(trace(matmul(target_state.data, status_fin[idx].data)))

        return loss, status_fin

Lastly, minimize the loss function with gradient-based optimization methods.

ITR = 100    # Number of iterations
LR = 0.2     # Learning rate
paddle.seed(999)

net = LOCC()
# Choose Adam optimizer
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.cir1.parameters() + net.cir2.parameters())

# Optimization loop
for itr in range(ITR):
    loss, status_fin = net.New_Protocol()
    # Backpropagation
    loss.backward()          
    opt.minimize(loss)
    # Clean gradients
    opt.clear_grad()
    # Print training result
    if itr % 10 == 0:
        print("itr " + str(itr) + ":", loss.numpy()[0])

# Calculate input state fidelity
fidelity_in = (3 * 0.7 + 1) / 4
# Calculate output state fidelity
fidelity = (len(status_fin) - loss) / len(status_fin)
# Calculate successful rate
suc_rate = sum([s.prob for s in status_fin])

print("The fidelity of the input quantum state is：%.5f" % fidelity_in)
print("The fidelity of the purified quantum state is： %.5f" % fidelity.numpy()[0])
print("The probability of successful purification is：%.5f" % suc_rate.numpy()[0])
rho_out = status_fin[0]
print("========================================================")
print(f"The output state is:\n {np.around(rho_out.data.numpy(), 4)}")
print(f"The initial logarithmic negativity is: {logarithmic_negativity(isotropic_state(2, 0.7)).numpy()[0]}")
print(f"The final logarithmic negativity is: {logarithmic_negativity(rho_out).numpy()[0]}")

itr 0: 5.7033257
itr 10: 1.552211
itr 20: 0.8980296
itr 30: 0.7061223
itr 40: 0.57139534
itr 50: 0.5278059
itr 60: 0.5121539
itr 70: 0.50759834
itr 80: 0.5052042
itr 90: 0.50493234
The fidelity of the input quantum state is：0.77500
The fidelity of the purified quantum state is： 0.93690
The probability of successful purification is：0.38654
========================================================
The output state is:
 [[ 4.790e-01-0.e+00j -1.000e-04-0.e+00j  1.000e-04-0.e+00j
   4.579e-01+5.e-04j]
 [-1.000e-04+0.e+00j  2.100e-02+0.e+00j  0.000e+00+0.e+00j
  -1.000e-04+0.e+00j]
 [ 1.000e-04+0.e+00j  0.000e+00-0.e+00j  2.100e-02+0.e+00j
   1.000e-04+1.e-04j]
 [ 4.579e-01-5.e-04j -1.000e-04-0.e+00j  1.000e-04-1.e-04j
   4.790e-01-0.e+00j]]
The initial logarithmic negativity is: 0.6322681307792664
The final logarithmic negativity is: 0.9059638381004333

Conclusion

As we can see, this new distillation protocol can purify four copies of isotropic states, each with a fidelity of 0.775, into a single two-qubit state with a fidelity of 0.937, which outperforms the extended DEJMPS protocol [3] with a distillation fidelity of 0.924 under the same setting. At the same time, our framework also exhibits advantages in terms of flexibility and scalability. With the help of LOCCNet, one can try various combinations and see what's the effect of increasing the communication rounds $r$, adding non-identical noisy entanglement before distillation, and importing different noise types.

LOCCNet has a wide range of applications, and distillation is merely one of them. We want to point out that the protocols trained by LOCCNet are hardware efficient since every operation is applicable in near term quantum devices, and we offer the possibility of customizing QNN architectures. Now, it's time to design and train your own LOCC protocol!

---

References

[1] Chitambar, Eric, et al. "Everything you always wanted to know about LOCC (but were afraid to ask)." Communications in Mathematical Physics 328.1 (2014): 303-326.

[2] Bennett, Charles H., et al. "Purification of noisy entanglement and faithful teleportation via noisy channels." Physical Review Letters 76.5 (1996): 722.

[3] Deutsch, David, et al. "Quantum privacy amplification and the security of quantum cryptography over noisy channels." Physical Review Letters 77.13 (1996): 2818.