LOCCNet: A Machine Learning Framework for LOCC Protocols¶

Overview¶

Quantum entanglement is an essential physical resource for quantum communication, quantum computation, and many other quantum technologies. Therefore, the ability to manipulate quantum entanglement reliably is an essential task if we want to build real applications in those fields. In the Noisy Intermediate-Scale Quantum (NISQ) era, directly transferring quantum information between the communication nodes inside a quantum network is an arduous task. Hence, the most natural set of operations to manipulate entanglement at this stage is the so-called Local Operations and Classical Communication (LOCC) [1] instead of global operations. Under this setup, several spatially separated parties can only implement local operations in their own labs and later communicate their measurement results (classical information) through a classical channel. Still, it is very challenging to design LOCC protocols for entanglement manipulation and further distributed quantum information processing tasks since the structure of LOCC is in general complicated and hard to characterize mathematically. To better explore the possibilities of near-term entanglement manipulation and long-term quantum information processing, we introduce LOCCNet, a machine learning framework for LOCC protocol design [2].

What is LOCC?¶

As we explained above, LOCC stands for Local Operations and Classical Communication. It is also known as the "distant lab" paradigm, where a multipartite quantum system is distributed to some spatially separated labs. Suppose there are $N$ labs involved, and each lab is allowed to implement a sequence of quantum operations $\{\mathcal{E}^{(k)}_j\}_{j=0}^{r}$ with respect to their own subsystems $k \in [1,\cdots,N]$. These labs are allowed to communicate any classical data including all the measurement results. A general LOCC protocol can be categorized according to the communication rounds $r$ applied and the number of distant labs involved, denoted as LOCC$_r(N)$, and pictorially described by a tree graph. For example, the famous quantum teleportation protocol [3] belongs to the 1-round LOCC$_1(2)$ family where only two parties are involved (Alice and Bob). The basic idea is to transfer an unknown quantum state $|\psi\rangle$ from Alice to Bob and the workflow is summarized in Figure 1,

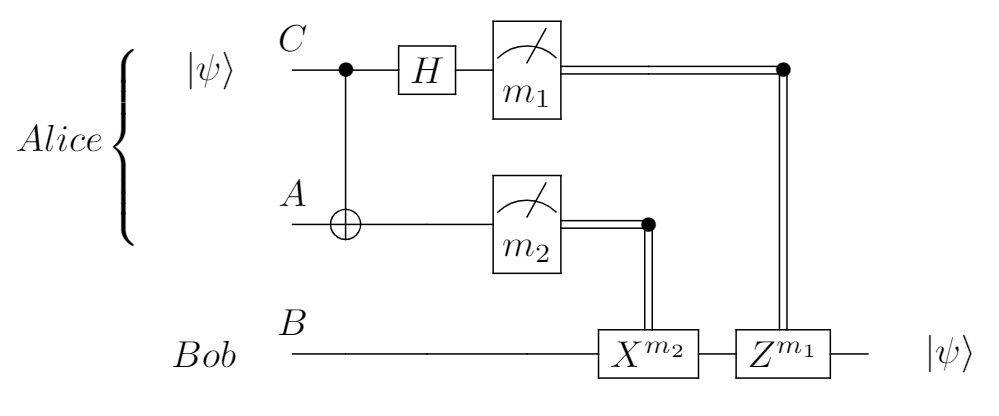
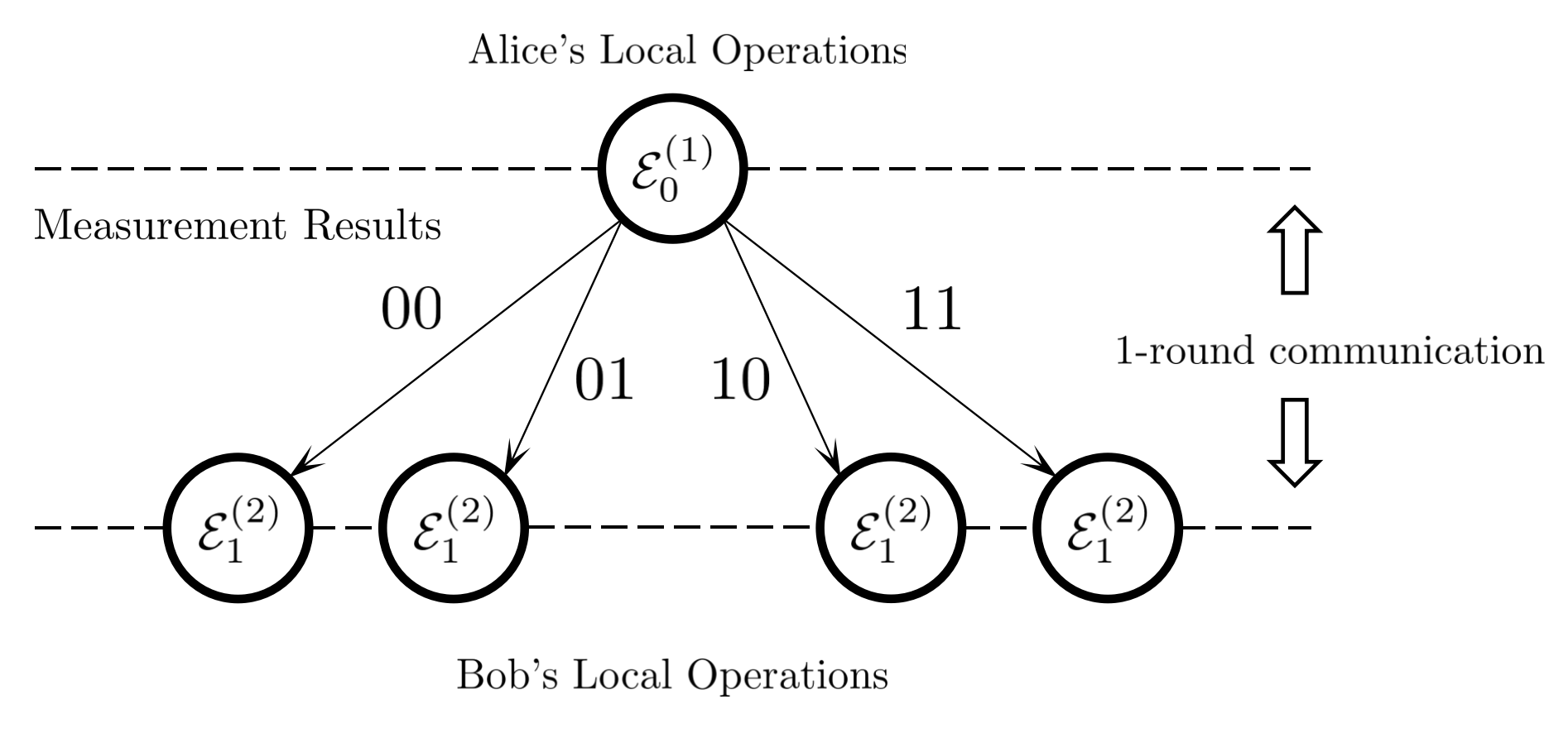
No description has been provided for this image

Figure 1. Quantum teleportation as an LOCC protocol presented in a circuit diagram (left) and a tree graph (right), where $m_1, m_2 \in \{0,1\}$.

In quantum teleportation, only Alice measures her qubits and Bob's local operations are completely decided by Alice's measurement results $m_1m_2 \in \{00,01,10,11\}$. We call this type of LOCC protocols as the control-type when the measurement results from $k^\text{th}$ party, a classical bit string $m_1m_2...m_n$, controls the subsequent local operations in each party ($k^\text{th}$ party measures $n$ qubits). For simplicity, we would not discuss the case when there exists multiple controllers. Things could be very different when Alice and Bob both measure their subsystem. They can choose to cooperate with each other and decide what to do next. For example, the following cooperation-type LOCC protocol shown in Figure 2 is proposed for entanglement distillation. We refer all the details to another tutorial on the BBPSSW protocol.

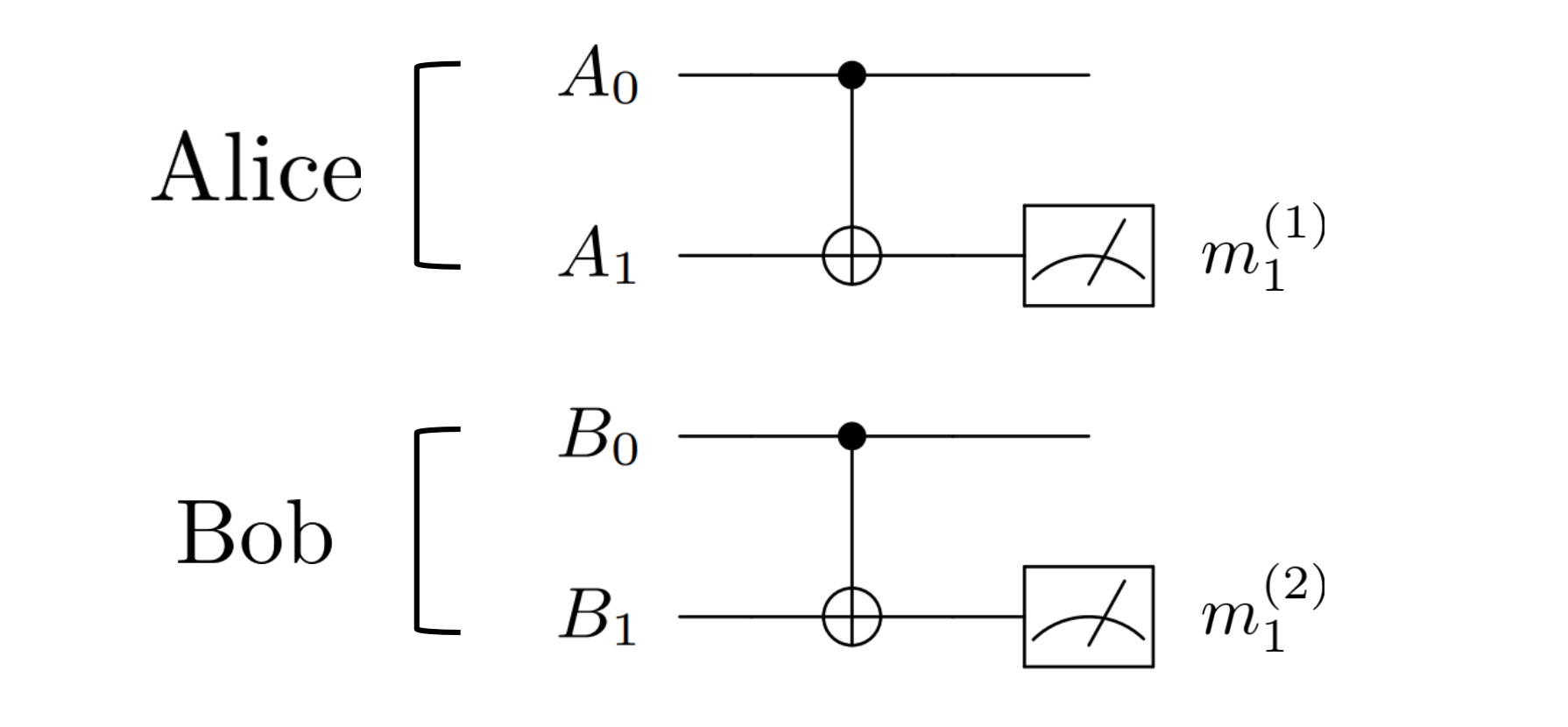
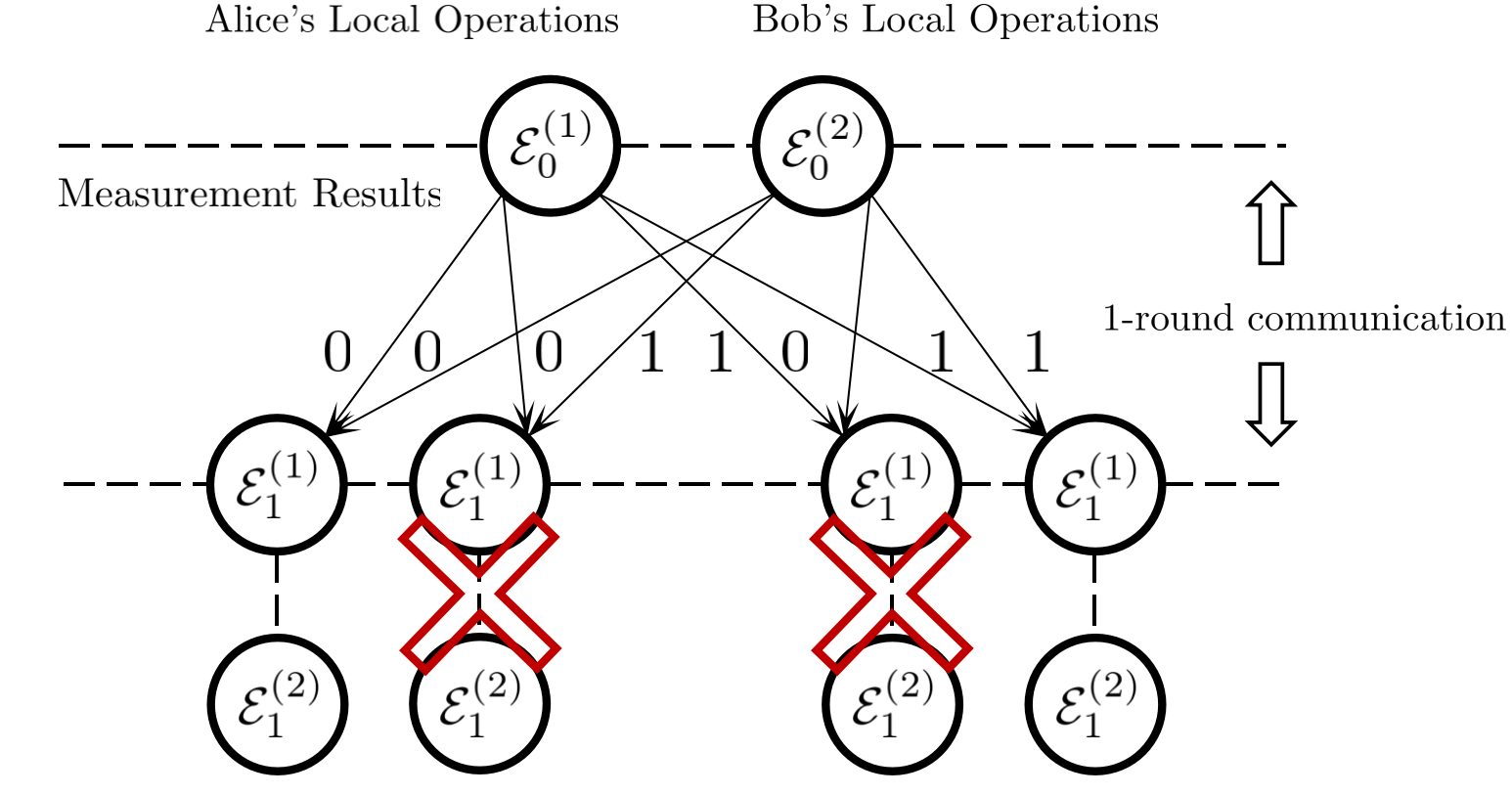
No description has been provided for this image

Figure 2. The BBPSSW distillation protocol as a cooperation-type LOCC protocol presented in a circuit diagram (left) and a tree graph (right), where $m_1^{(1)}, m_1^{(2)} \in \{0,1\}$. The notation $m_j^{(k)}$ refers to the measurement result on qubit $j$ of the $k^\text{th}$ party. The protocol fails when $m_1^{(1)}m_1^{(2)} \in \{01,10\}$. Here, $\mathcal{E}_{0}^{(1)} = \mathcal{E}_{0}^{(2)} = \text{CNOT}$ and $\mathcal{E}_{1}^{(1)} = \mathcal{E}_{1}^{(2)} = I$.

These protocols look quite simple, but things could become extremely complicated when many parties communicate with each other for multiple rounds and we still need to find out the best local operations each party should apply in each round. Now, we should at least have a taste of why designing an LOCC protocol is challenging. With such difficulty, many practical LOCC protocols have been purposed to fulfill meaningful tasks including entanglement distillation [4-5], entanglement swapping [6-7], and so on.

Philosophy of LOCCNet¶

Inspired by the success of Machine Learning (ML) in solving the quantum many-body problem [8] and protein folding structure prediction [9], we would like to adopt the learning capability of ML to help search optimal LOCC protocols among many possible combinations. The basic idea of LOCCNet is to utilize quantum neural networks (QNNs) to represent each local quantum operation $\mathcal{E}^{(k)}_j$. That means each node represented in the tree graph of an LOCC protocol is now replaced by a QNN, which is essentially a parameterized quantum circuit (PQC) denoted by $U(\boldsymbol \theta)$. In Paddle Quantum, we already provide many QNN templates to reduce the learning cost for users. Once we set up the QNN, we can freely choose the measurement and communication plan. One last recipe we would need is a learning objective which is usually encoded as a loss function $L$. For example in quantum teleportation, the learning objective could be maximizing the state fidelity between Alice's state $|\psi\rangle$ and the state Bob receives $|\phi\rangle$ under four possible measurement results, meaning that $L \equiv \sum_{m_1m_2} \big(1- F(|\psi\rangle, |\phi\rangle)\big)$. The loss function should be designed according to the specific goal we want to accomplish. Finally, classical optimization methods (mainly gradient-based) will be applied to train the parameters in each QNN. Once the optimization has been done, we could obtain a near-optimal LOCC protocol. From our perspective, such a framework could sharply reduce the efforts to develop novel LOCC protocols, and the results should be easy to verify by experiments.

Note: LOCCNet only supports density matrix formulation at the current version.

Building blocks¶

In this section, we will introduce all the main building blocks of LOCCNet to give users a taste on what our framework can achieve. We firstly present a piece of pseudo code:

from paddle_quantum.locc import LoccNet

class Net(LoccNet):
    def __init__(self):
        super(Net, self).__init__()
        # Step 0: System initialization 
        # Step 1: Set up the initial quantum states
        # Step 2: Define QNNs

    def forward(self):
        # Step 3: Execute QNNs
        # Step 4: Measurement
        # Step 5: Calculate the loss function
        return loss, final_status

Firstly, we need to create a python class through class Net(LoccNet) to reserve the complete quantum system and many helpful functions will be inherited from LoccNet. The main body of an LOCC protocol is realized in this customized class Net() which consists of two functions -- __init__() and forward(). In the __init__() function, you can initialize all the remote parties, quantum state in each subsystem, and the QNNs.

self.add_new_party(qubits_number, party_name=None) is used to add one party, the first parameter means the number of qubits held by this party; the second parameter is optional, which stands for the party's name. In a protocol, you can choose to identify each party either by their name character ID or a number ID. If you want to use the mode of character, you need to specify party_name when calling add_new_party; if you choose the latter mode, you don't need to set them, and the numbers will increase from 0 in the order you add them.
self.set_init_state(state, which_qubits) is used to set the initial quantum state to be processed by your protocol. Here state is always in density matrix formulation, and which_qubits represents the identification of quantum states (belong to which qubits held by certain parties). It should be noted that you must give all the qubits to the initial quantum state through this function. Otherwise, the program will occur unexpected errors.
self.create_ansatz(party_id) is to create the local quantum circuit of some party, hence you should specify the party through party_id. For example, cir1 = self.create_ansatz("Alice")creates a circuit belonging to Alice, and we can manipulate Alice's qubits through this circuit, add X gates, add CNOT gates, and so on.

In the forward() function, we can define the specific workflow of the protocol. If you want to train a model, you need to define the loss function as the return value of the function forward() which will be minimized by updating the trainable parameters. If you just want to verify the result of a protocol, you don't need to define the loss function and can return the object of interests, such as the final quantum state, the probability to get reach that state, and so on. Generally, we mainly perform two operations in the function forward(), quantum operations and measurement. We also provide corresponding functions for these two operations:

Execute quantum circuits to obtain the output result, e.g., status_out = cir1(status).
self.measure(status, which_qubits, results_desired, theta=None) is the measurement function we provided in LoccNet. The status is the LoccStatus you want to measure, which we will introduce below. which_qubits means the qubits you want to measure. If you want to measure Alice's 0th qubit, just assign which_qubits to ("Alice", 0). If you want to measure Alice's 0th qubit and Bob's 1st qubit at the same time, you can assign which_qubits to [("Alice", 0), ("Bob", 1)]. results_desired is the measurement result you want, it can only include "0", "1", or ["0", "1"]. theta means the parameter of parameterized measurement, which you don't need to provide if you want to measure without parameter.
LoccStatus: In LoccNet, the smallest information processing unit we use is not a quantum state, but something we call the LoccStatus. It includes quantum state, the probability from the initial situation to this state, and the measurement results in this process. Sometimes, the state you want to get is not single, which means there are many situations in this protocol that are considered successful. We can also meet this demand. In the function self.measure()，if the parameter results_desired you give is a list, which means you want to get several LoccStatus, it would return a list of LoccStatus.

Welcome aboard!¶

After introducing all the necessary components of LOCCNet, we suggest starting with one of following tutorials and build a deeper understanding with coding:

What LOCCNet can do is far more than the listed topics. We encourage you to explore more possibilities with this new framework!

References¶

[1] Chitambar, Eric, et al. "Everything you always wanted to know about LOCC (but were afraid to ask)." Communications in Mathematical Physics 328.1 (2014): 303-326.

[2] Zhao, Xuanqiang, et al. "Practical distributed quantum information processing with LOCCNet." npj Quantum Information 7, 159 (2021).

[3] Bennett, Charles H., et al. "Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels." Physical Review Letters 70.13 (1993): 1895.

[4] Bennett, Charles H., et al. "Purification of noisy entanglement and faithful teleportation via noisy channels." Physical Review Letters 76.5 (1996): 722.

[5] Deutsch, David, et al. "Quantum privacy amplification and the security of quantum cryptography over noisy channels." Physical Review Letters 77.13 (1996): 2818.

[6] Zeilinger, Anton, et al. "Three-particle entanglements from two entangled pairs." Physical Review Letters 78.16 (1997): 3031.

[7] Zukowski, Marek, et al. "" Event-ready-detectors" Bell experiment via entanglement swapping." Physical Review Letters 71.26 (1993).

[8] Carleo, Giuseppe, and Matthias Troyer. "Solving the quantum many-body problem with artificial neural networks." Science 355.6325 (2017): 602-606.

[9] Senior, Andrew W., et al. "Improved protein structure prediction using potentials from deep learning." Nature 577.7792 (2020): 706-710.