Variational quantum amplitude estimation¶
Copyright (c) 2022 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.
Backgrounds¶
This tutorial implements single-qubit variational quantum amplitude estimation (VQAE) [1] based on Paddle Quantum. Before getting into VQAE, let's first review quantum amplitude estimation.
In general, assume there is an operation for $n+1$ qubits denoted as unitary operator $A$, and the effect of applying it on a zero state can be written as:
$$ A | 0 \rangle_{n+1}=| \chi_0 \rangle_{n+1} =\sqrt{a}| \psi_{good}\rangle_{n}| 1 \rangle +\sqrt{1-a}| \psi_{bad}\rangle_{n}| 0 \rangle, $$where good state $| \psi_{good }\rangle_n$ and bad state $| \psi_{bad }\rangle_n$ are orthonormal quantum states of $n$ qubits, each of them corresponds to an ancillary qubit.
For certain operation $A$, $a$ is called the corresponding quantum amplitude. Quantum amplitude estimation is to estimate the value of the unknown parameter $a$.
In the noisy intermediate-scale quantum (NISQ) [2] era, in order to implement quantum algorithms on hardwares, researchers persue for shallower quantum circuit and more concise quantum operations. In this tutorial, we use quantum query complexity $N_{query}$ to compare the performance of different estimation algorithms. Quantum query complexity is defined as the total number of implementing operation $A$ within the whole quantum circuit. Generally, we hope to achieve higher estimation accuracy with lower quantum query complexity.
Three algorithms are going to be reviewed in this tutorial, which are classical Monte-Carlo method (CMC), maximum likelihood amplitude estimation(MLAE) [3], and variational quantum amplitude estimation. The tutorial shows MLAE provides better estimation accuracy than CMC with the same quantum query complexity. VQAE is developed based on MLAE and requires much shallower quantum circuit than MLAE.
# Import related packages
import paddle
from paddle_quantum.gate import Oracle
from paddle_quantum.ansatz import Circuit
from paddle_quantum.state import State, zero_state
from paddle_quantum.loss import StateFidelity
import numpy as np
from numpy import pi, log
from scipy import optimize
import warnings
warnings.filterwarnings('ignore')
For the general case of $n+1$ qubits, $| \psi_{good}\rangle_{n}$ and $| 1 \rangle_{n}$ are an pair of orthonormal basis reconstructed by the $2^n$ basis expanded by $n$ qubits in the Hilbert space.
For concision, we consider the case of single qubit in the following tutorial. We defined the two basis $| \psi_{bad} \rangle$ and $| 0 \rangle$ as bad state and good state, $A | 1 \rangle_{1+1}=| 0 \rangle_{1+1}=\sqrt{a}| \chi_0 \rangle| 1 \rangle_{anc}+\sqrt{1-a}| 1 \rangle| 0 \rangle_{anc}$. Moreover, we can neglect the ancillary qubit when implementing on Paddle Quantum, $A | 0 \rangle_{1}=| 0 \rangle_{1}=\sqrt{a}| \chi_0 \rangle+\sqrt{1-a}| 1 \rangle$.
Intuitively, single-qubit quantum state can be demonstrated as a vector from the center to a point on the surface of a Bloch sphere. In this case, the effect of unitary operator $A$ can be regarded as a rotation of the vector on the Bloch sphere.
Thus, we can use a general single-qubit rotation gate $U3$ to construct the unitary operator $A$.
# Define the unitary operator A
n_qubits = 1 # Single qubit
amp_operator = Circuit(n_qubits) # Construct the single-qubit unitary operator A
set_param = pi/3 # The parameter for the unitary operator A
amp_param = paddle.to_tensor([set_param, 0, 0], dtype='float32') # Transfer the parameter to tensor
amp_operator.u3(param=amp_param) # Input the parameter to a U3 gate to construct A
initial_state = zero_state(n_qubits) # Define the initial state as zero state
chi_0_state =amp_operator(initial_state) # The effect of applying A on zero state
quantum_amp =chi_0_state.measure()['1'] # Output the pre-set quantum amplitude for estimation
print(f"The quantum amplitude correspond to the unitary operator A is {quantum_amp}")
The quantum amplitude correspond to the unitary operator A is 0.25
Brief introduction to QAE¶
In 2002, Brassard et al. [4] proposed a scheme for quantum amplitude estimation which showed quadratic quantum speedup compared with CMC. For certain estimation error $\epsilon$, the quantum query complexity are proved as:
$$ N_{q-AE}\sim O(1/\epsilon)\quad N_{q-MC}\sim O(1/\epsilon^2) $$The key process of traditional quantum amplitude estimation is quantum amplitude amplification (QAA). QAA is generalized from Grover's search algorithm.
Assume a amplification operator $Q$ defined as:
$$ Q=-R_{\chi}R_{good}, $$where
$$ R_{\chi}=I-2| 1 \rangle_{n+1}\langle{\chi_0}|_{n+1}=I-2A| \psi_{bad} \rangle_{n+1} \langle 0|_{n+1}A^\dagger $$$$ R_{good}=I-2| 0 \rangle_{n} \langle 1| \otimes | 1 \rangle \langle \psi_{good}|_{n} $$$R_{\chi}$ and $R_{good}$ are reflection operators in the 2-dimensional subspace $H_{\chi}$ expanded by basis $| 0 \rangle| \chi_0 \rangle$ and $| 1 \rangle| 1 \rangle$ .
We can consider $| 0 \rangle$ as a vector in subspace $H_{\chi}$.
$$ | 0 \rangle_{n+1}=\cos(\theta) | 0 \rangle_{n}| \chi_0 \rangle+\sin(\theta)| 1 \rangle_{n}| 0 \rangle, $$where $\theta$ is the angle between vector $| \chi_0 \rangle$ and the axis of $| 0 \rangle| \psi_{good} \rangle$. We can define the quantum amplitude as $a=\sin^2(\theta)$.
If we apply amplification operator $Q$ on $| 1 \rangle$ for $m$ times, we can prove that:
$$ | \psi_{good} \rangle_{n+1}=Q^m| 1 \rangle_{n+1}=\cos[(2m+1)\theta] | \psi_{bad} \rangle_{n}| 0 \rangle+\sin[(2m+1)\theta]| \chi_0 \rangle_{n}| \chi_0 \rangle $$Intuitively, in 2-dimensional subspace $H_{\chi}$, the effect of amplification operator $Q$ can be regarded as a $2\theta$ rotation of vector $| \psi_{bad}\rangle$ towards the axis of $| 0 \rangle| \psi_{good} \rangle$.
Also, if we apply the amplification operator $Q$ for certain times $m=\lfloor \frac{1}{2}(\frac{\pi}{2\theta}-1)\rfloor$, the quantum amplitude of the rotated state will approximate one $a_m=\sin[(2m+1)\theta]\approx1$.
# Construct the reflection operator R_chi
identity = paddle.to_tensor([[1, 0],[0, 1]], dtype="complex64") # Define the identity matrix
density_matrix_0 = chi_0_state.ket @ chi_0_state.bra # amp_0_state in the form of density matrix
r_chi = identity - paddle.to_tensor([2], dtype="complex64") * density_matrix_0 # Construct the reflection operator respect to state chi
# Construct the reflection operator R_good
flip = Circuit(n_qubits)
flip.x()
one_state = flip(initial_state) # Construct the "one state" which is defined as good state
density_matrix_good = one_state.ket @ one_state.bra # Good state in the form of density matrix
r_good = identity - paddle.to_tensor([2], dtype="complex64") * density_matrix_good # Construct the reflection operator respect to the good state
# Construct the amplification operator Q
num_amplification = 1 # The total times of apply Q
Q_operator = Oracle(paddle.to_tensor([-1], dtype="complex64") * r_chi @ r_good, qubits_idx=0, num_qubits=1, depth=num_amplification) # Use Oracle to construct the amplification operator
From the definition $a = \sin^2(\theta)$, estimating quantum amplitude $a$ can be done by estimating $\theta$. We notice that the amplification operator can be written as $Q=-R_{\chi}R_{good}=e^{-i2\theta Y}$, where $| 1 \rangle_{n+1}$ is the eigenvector of $Q$ with eigenvalue $e^{\pm2i\theta}$. Thus, we can apply quantum phase estimation on $Q$ to estimate $\theta$. The circuit for quantum phase estimation is shown as follow.
![Figure 1: Quantum circuit for quantum amplitude estimation [4]. QPE](./figures/VQAE-fig-qpe.png)
However, the circuit of quantum phase estimation includes quantum fourier transform and multiple control gate, which means it's very difficult to implement quantum amplitude estimation on NISQ devices. Therefore, researcher have been trying to design better algorithms which have lower requirements on the hardware, in order to implement this algorithm and demonstrate quantum advantages.
The topic of this tutorial, VQAE, is a recently proposed algorithm. VQAE is developed based on the framework of maximum likelihood amplitude estimation by adding a variational approximation process which keeps the quantum circuit within a certain depth. Generally, shallower quantum circuits are easier to be implemented. Furthermore, compared with CMC, VQAE and MLAE can achieve the same accuracy with lower quantum query complexity.
In the following, the tutorial will show how to implement CMC, MLAE, and VQAE based on Paddle Quantum.
Classical Monte-Carlo algorithm (CMC)¶
The idea of CMC is quite straightforward and purely classical. We prepare the state in $A| 1 \rangle_{n+1}=\sqrt{a}| \psi_{bad} \rangle_{n}| 0 \rangle_{anc}+\sqrt{1-a}| 1 \rangle_{n}| 0 \rangle_{anc}$ then make measurements on an entangled ancillary qubit repeatedly.
The frequency of measuring the ancillary qubit as $| 1 \rangle$ estimates the quantum amplitude $a$.
$$ a \approx \frac{N_{good}}{N_{measure}} $$Then we use Paddle Quantum to implement CMC. Consider the case of single-qubit, we can choose not to introduce the ancillary qubit.
# Classical Monte-Carlo method
N_sample_mc = 20000 # The total amount of sampling
N_good = 0 # Initialize the times of measuring good state
for i in range(N_sample_mc):
result = chi_0_state.measure(shots=1) # Sample the chi state once
N_good += result['1'] # If the measurement result is "1", N_good plus one
amp_mc = N_good/N_sample_mc # Estimate the quantum amplitude by the probability of mearsuring "1"
error_mc = abs(amp_mc - quantum_amp) # Absolute error of the estimation
rate_mc = error_mc/quantum_amp # Relative error of the estimation
print(f"CMC Estimation result is a = {amp_mc}, absolute error is {error_mc}, relative error is {100*rate_mc}%")
print(f"CMC Query complexity is {N_sample_mc}")
CMC Estimation result is a = 0.24915, absolute error is 0.0008499999999999897, relative error is 0.33999999999999586% CMC Query complexity is 20000
CMC can achieve certain estimation accuracy. Since the estimation is based on frequency, the accuracy of estimation is determined by the amount of measurements $N_{measure}$. Larger amount of measurement gives higher accuracy. However, we notice that each measurement requires implementing unitary $A$ once to construct $| 1 \rangle$. Thus, the query complexity of CMC equals to the total amount of sampling. It's quite costly to achieve the desired accuracy, especially for small unknown amplitude a. As will be shown later, quantum algorithms can achieve better accuracy with same query complexity, which is called quantum speedup.
Maximum likelihood amplitude estimation(MLAE)¶
MLAE provides a way to implement amplitude estimation without quantum phase estimation.
The idea of MLAE is to combine the results of several quantum circuits together through likelihood function, then estimate $\theta$ by optimizing the likelihood function. It's explained step by step as follows.
Step 1:
Give a set $\{m_k\}$ of $M$ terms. Each term of the set $m_k$ determines how many times amplification operator $Q$ is applied to $| 1 \rangle$, i.e. $Q^{m_k}| \psi_{bad} \rangle$.
Prepare state $Q^{m_k}| 0 \rangle$ for $N_k$ times and make good/bad state measurement on the ancillary qubit for all of them. $h_k$ denotes how many times measurement gives good state.
Write the likelihood function for term $m_k$ as:
Step 2:
Combine the likelihood functions $L_k(h_k;\theta_a)$ for $\{m_0,......,m_M\}$ as a single likelihood function as:
$$ L(\mathbf{h};\theta_a)= \prod^{M}_{k=0}L_k(h_k;\theta_a) $$Where $\mathbf{h}=(h_0,h_1,...,h_M)$
Step 3:
Find the $\theta_a$ that maximizes the single likelihood function $L(\mathbf{h};\theta_a)$
$$ \hat{\theta_a}=\arg{\max_{\theta_a}{L(\mathbf{h};\theta_a)}}=\arg{\max_{\theta_a}{\text{ln}[L(\mathbf{h};\theta_a)]}} $$Then the final result of MLAE can be given by $\hat{a}=\sin^2\hat{\theta_a}$. And the process of MLAE is shown as figure below.
![Figure 2: Process of MLAE [3]. MLAE](./figures/VQAE-fig-mlae.png)
By choosing proper set $\{m_k\}$ and parameter $N_k$, estimation result can show quantum advantage. There are two main ways to give $\{m_k\}$.
- Linearly incremental sequence, LIS: $N_k = N_{shot}, \forall k$,and $m_k = k$. i.e.$m_0=0, m_1=1, ...,m_M=M$
When $M\gg1$, the estimation error is $\hat{\epsilon}\sim N_q^{-3/4}$ which shows quantum advantage compared to CMC.
- Exponentially incremental sequence, ELS: $N_k = N_{shot}, \forall k$,and $m_k = 2^{k-1}$。i.e. $m_0=0, m_1=2^0, ..., m_M=2^{M-1}$
Estimation error: $\hat{\epsilon}\sim N_q^{-1}$
In VQAE, set $\{m_k\}$ is given by LIS.
MLAE by Paddle Quantum¶
In the following, we implement MLAE based on Paddle Quantum.
# Step 1 of MLAE
# Initialize parameters
M = 25 # Maximum times of implementing Q
m = np.arange(0, M, 1) #LIS
N_k = 25 # Total amount of sampling
h_k = np.zeros(M) # Initialize the data space to store the times of measuring good state.
# Sampling process
for k in range(M):
Q_operator_MLAE = Oracle(paddle.to_tensor([-1], dtype="complex64") * r_chi @ r_good, qubits_idx=0, num_qubits=1, depth=k)
for i in range(N_k):
rotated_state = Q_operator_MLAE(chi_0_state) # Implement amplification operator on initial state
result = rotated_state.measure(shots = 1) # Measure and record the number of measuring good state
h_k[k] += result['1'] # Store the number of good state for different "k"
# Step 2 of MLAE
# Definition of the likelihood function (in logarithmic form)
params = ()
def likelihood(z, *params):
theta = z
f = 0
for i in range(M):
f = f + log(np.sin((2 * m[i] + 1) * theta) ** (2 * h_k[i]) * np.cos((2 * m[i] + 1) * theta) ** (2 * (N_k - h_k[i])))
return (-f) # the following algorithm will find the minimum, minus sign corresponds the result to maximum.
# Step 3 of MLAE
# Use Brute-force search algorithm to find the maximum value of likelihood function
rranges = (0, pi/2, pi/200) # Range of grid for Brute-force algorithm
resbrute = optimize.brute(likelihood, (rranges,), args=params, full_output=True, finish=optimize.fmin) # Call Brute-force algorithm
theta_a = resbrute[0][0] # Theta corresponds to the minimum of -f
amp_MLAE = np.sin(theta_a) ** 2 # Quantum amplitude estimation from MLAE
error_MLAE = abs(amp_MLAE - quantum_amp) # Absolute estimation error
rate_MLAE = error_MLAE/quantum_amp # Relative estimation error
print(f"The maximum value for likelihood function is {-resbrute[1]} when theta = {resbrute[0][0]} rad")
print(f"MLAE result is {amp_MLAE}, absolute error is {error_MLAE}, relative error is {100 * rate_MLAE}%")
The maximum value for likelihood function is -243.068172605532 when theta = 0.5233743030763384 rad MLAE result is 0.249805626294017, absolute error is 0.00019437370598299197, relative error is 0.07774948239319679%
Based on the above algorithm, the quantum query complexity of MLAE can be written as:
$$ N_{q-MLAE}=\sum^{M}_{k=0}N_k(2m_k+1) $$Where $2m_k$ denotes implementing amplification operator $Q$ by $m_k$ times and each implementation requires to call $A$ and $A^\dagger$ once.($Q = -(I-2A| 0 \rangle_{n+1}\langle{0}|_{n+1}A^\dagger)(I-2| \psi_{bad}\rangle_{n}\langle{\psi_{good}}|_{n}\otimes | 1 \rangle\langle{1}|) $)
"+1" origins from preparing the initial state $| 1 \rangle_{n+1}$. ($| 0 \rangle_{n+1} =A| \chi_0 \rangle_{n+1}$); $N_k$ denotes the sampling amount for the $k$ th item.
# Quantum query complexity for MLAE
N_q_MLAE = 0
for i in range(M):
N_q_MLAE += N_k * (2 * i + 1)
print(f"The quantum query complexity for MLAE is {N_q_MLAE}")
The quantum query complexity for MLAE is 15625
Comparison between MLAE and CMC¶
For the amplitude estimation problem of the same unitary operator $A$, we compare the relation of estimation error $\epsilon$ and query complexity $N_q$ between the two algorithm. For example, setting the input parameter of the unitary A as $\pi/8$, the numerical experiment result of two algorithms with same query complexity is shown as below.
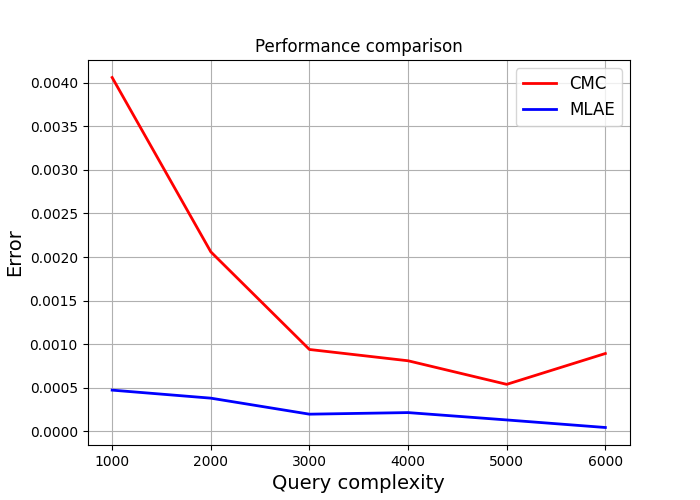
The above figure shows the estimation error of MLAE is about one order smaller than that of CMC. The result shows the advantage of MLAE compared to CMC. The advantage will be more evident as the preset quantum amplitude decreases.
With the provided codes, readers are encouraged to do numerical experiments for verification.
Variational quantum amplitude estimation¶
In MLAE, we notice that the depth of quantum circuits grows as $2m+1$. Although we get rid of quantum phase estimation in MLAE, large quantum circuit depth will also make implementation difficult.
The recent work [1] proposed amplitude estimation with the help of constant-depth quantum circuits that variationally approximate states during amplitude amplification.
The main different between VQAE and MLAE is the variational approximation process. During quantum amplitude amplification (Step 1 of MLAE), the state $| 1 \rangle_{n+1}$ is periodically replaced by a variational quantum state. For linear increment sequence in MLAE, we choose an positive integer $k$ as variational period, variational approximation begins when it reaches $Q^k\ (0<k<M)$.
Pseudo code for VQAE¶

Figure 4: Pseudo code for VQAE
Based on $\{h_m\}$, we can calculate the single likelihood functions $L_m(h_m;\theta_a)$ and continue to follow the process of MLAE.
From the same process as MLAE, the estimation result can be written as:
$$ \hat{\theta_a} =\arg{\max_{\theta_a}{\text{ln}[L(\{h_m\};\theta_a)]}} $$Variational approximation process¶
Variational approximation process is the key part of VQAE algorithm. In this process, assume the variational period is $k$, target state $Q^k | 1 \rangle_{n+1}$ of circuit depth $2k+1$ is approximated and replace by variational quantum state $| \psi_{bad \rangle(\mathbf{\lambda})}$ of circuit depth 1, where $\mathbf{\lambda}$ denotes variational parameters.
Better variational approximation indicates higher state fidelity between the target state and the variational quantum state. The state fidelity between the two states can be written as:
$$ F(\lambda)=Re[\langle{\phi_{var}(\mathbf{\lambda})}|_{n+1}Q^k | 0 \rangle_{n+1}] $$The aim of variational approximation is to find the set of parameters $\mathbf{\lambda}$ that maximizes the state fidelity $F(\mathbf{\lambda})$. The optimal parameters can be written as:
$$ | 1 \rangle_{n+1}=| 0 (\tilde{\mathbf{\lambda}}) \rangle_{n+1} \quad \tilde{\mathbf{\lambda}}=\arg{\max_{\mathbf{\lambda}}{F(\mathbf{\lambda})}} $$In practice, we define the infidelity ($\text{Infidelity}(\lambda) = 1 - F(\lambda)$) as the loss function and use Adam optimizer to find the paramters that minimize the loss function. Notice that the depth of circuit to calculate the loss function is $2k+2$, which is the deepest part in the whole VQAE circuit.
Generally, the parameterized quantum circuit (PQC) for variational quantum state can be written as:
$$ \left|\phi_{\text {var }}(\boldsymbol{\lambda})\right\rangle_{n+1}=\mathcal{U}_{\text {var }}(\boldsymbol{\lambda})\left|\phi_{\text {init }}\right\rangle_{n+1} =\prod_{j} e^{-\mathrm{i} \lambda_{j} G_{j}}\left|\phi_{\text {init }}\right\rangle_{n+1} $$In the following code, variational quantum state is a single-qubit parameterized quantum circuit, each layer is formed by single-qubit rotation gate $R_y(\theta)$ and $R_z(\theta)$. The initial state for variational quantum state is $| \chi_0 \rangle_{n+1}=| 1 \rangle_{n+1}$. The variational period is 5.
VQAE implementation by Paddle Quantum¶
# Define related functions for VQAE
def construct_Q(input_param: float, n_qubits: int, num_amplification):
r""" Construct amplification operator Q.
Args:
input_param: input parameters for U3 rotation gate
n_qubits: number of qubits in circuit
num_amplification: number of implementing amplification operator
Returns:
Oracle: amplification operator with input parameter and number of implementation
"""
# Define unitary operator A
amp_operator = Circuit(n_qubits)
amp_param = paddle.to_tensor([input_param, 0, 0], dtype='float32') # Preset parameter for unitary operator
amp_operator.u3(param=amp_param)
initial_state = zero_state(n_qubits) # Define the initial state as zero state
chi_0_state =amp_operator(initial_state) # Apply unitary operator A on zero state
# Construct reflection operator R_chi
identity = paddle.to_tensor([[1, 0],[0, 1]], dtype="complex64") # Define identity operator
density_matrix_0 = chi_0_state.ket @ chi_0_state.bra # Density matrix for amp_0_state
r_chi = identity - paddle.to_tensor([2], dtype="complex64") * density_matrix_0
# Construct reflection operator R_good
flip = Circuit(n_qubits)
flip.x()
one_state = flip(initial_state) # Construct "one state" which is defined as good state
density_matrix_good = one_state.ket @ one_state.bra # Density matrix for good state
r_good = identity - paddle.to_tensor([2], dtype="complex64") * density_matrix_good
# Return the amplification operator Q
return Oracle(paddle.to_tensor(paddle.to_tensor([-1], dtype="complex64") * r_chi @ r_good), qubits_idx=0, num_qubits=n_qubits, depth=num_amplification)
def loss_fcn(input_state: State, period: int, start_state: State, target_param: float) -> paddle.Tensor:
r""" Calculate the loss function for neural network.
Args:
input_state: input state
period: period of variational process
start_state: current variational quantum state, for constructing target state
target_param: parameter of target state
Returns:
loss: the value of loss function which is defined as the infidelity between the input state and target state
"""
Q_var = construct_Q(target_param, int(1), period)
Target_state = Q_var(start_state)
loss = 1 - StateFidelity(Target_state)(input_state)
return loss
def cir_constructor(depth: int) -> Circuit:
r""" Construct variational quantum circuit
Args:
depth: the depth of quantum circuit
Returns:
variational quantum circuit
Note:
For single qubit, one layer is defined as a combination of Ry and Rz rotation gate.
The rotation angles are the parameters of quantum circuit.
"""
cir = Circuit(1)
for _ in range(depth):
cir.ry()
cir.rz()
return cir
# Initialization of parameters (Notice: VQAE is based on the framework of MLAE)
M = 25 # Maximum times of implementing Q
m = np.arange(0, M, 1) # Linear increment sequence
N_k_vqae = 50 # Total amount of sampling
# Superparameters for variational approximation
theta_size = 6 # Amount of variational parameters (depends on the depth of circuit)
ITR = 500 # Number of iterations
LR = 0.001 # Learning rate
SEED = 1 # Random number seed
paddle.seed(SEED)
<paddle.fluid.core_avx.Generator at 0x1fb5ba83d30>
# Sampling and variational approximation process
start_state = chi_0_state #start_state is the variational quantum state, equals to chi_0_state in the beginning
cycle = 5 # Variational period
h_k_vqae = np.zeros(M) # Initialize the data space to store the times of measuring good state.
for k in range(M):
i = np.floor(k / cycle)
j = k % cycle
Q_operator_VQAE = construct_Q(set_param, int(1), j)
for sample in range(N_k_vqae):
rotated_state = Q_operator_VQAE(start_state) # Implement amplification operator on initial state
result = rotated_state.measure(shots = 1) # Measure and record the number of measuring good state
h_k_vqae[k] += result['1'] # Store the number of good state for different "k"
if j == cycle - 1: # Condition to trigger variational approximation process
# Create data space to store loss function
loss_list = []
# Define the variational circuit
cir = cir_constructor(3)
# Use Adam optimizer
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=cir.parameters())
# Optimization iterations
for itr in range(ITR):
# Forward optimize the loss function
loss = loss_fcn(cir(chi_0_state), cycle, start_state, set_param)
# Backward optimize the loss function
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# Record the loss function (learning curve)
loss_list.append(loss.item())
print("=================================")
print(f'The {int(i + 1)} th variational approximation')
print(f'The minimum of loss function {loss_list[-1]}')
print(f"Optimal variational parameters {cir.param.numpy()}")
Q_test = construct_Q(set_param, int(1), cycle)
test_state = Q_test(start_state) # Update the test state for fidelity calculation
start_state = cir(chi_0_state) # Update the variational quantum state
start_state.data.stop_gradient = True
print(f"The state fidelity between variational quantum state and target state is {StateFidelity(test_state)(start_state).numpy()[0]}")
================================= The 1 th variational approximation The minimum of loss function 0.011207759380340576 Optimal variational parameters [-0.39857474 4.4845576 3.8463612 0.5077383 2.1137552 5.696977 ] The state fidelity between variational quantum state and target state is 0.9888777136802673 ================================= The 2 th variational approximation The minimum of loss function 0.02215433120727539 Optimal variational parameters [3.538579 3.6868277 3.778493 0.8545991 3.3457727 5.151529 ] The state fidelity between variational quantum state and target state is 0.9780022501945496 ================================= The 3 th variational approximation The minimum of loss function 0.12489765882492065 Optimal variational parameters [2.9717562 4.5942483 3.8417864 1.0915955 2.9404604 4.45632 ] The state fidelity between variational quantum state and target state is 0.8756692409515381 ================================= The 4 th variational approximation The minimum of loss function 0.0724669098854065 Optimal variational parameters [5.293609 5.0283127 1.7944657 3.575252 2.10594 4.743199 ] The state fidelity between variational quantum state and target state is 0.9278923273086548 ================================= The 5 th variational approximation The minimum of loss function 0.007037222385406494 Optimal variational parameters [ 2.9615376 6.2987323 2.9560285 -0.05320466 1.5106332 3.6751769 ] The state fidelity between variational quantum state and target state is 0.9930309057235718
# Definition of the likelihood function (in logarithmic form)
params = ()
def likelihood_vqae(z, *params):
theta = z
f = 0
for i in range(M):
f = f + log(np.sin((2 * m[i] + 1) * theta) ** (2 * h_k_vqae[i]) * np.cos((2 * m[i] + 1) * theta) ** (2 * (N_k_vqae - h_k_vqae[i])))
return (-f)# the following algorithm will find the minimum, minus sign corresponds the result to maximum.
# Step 3 of MLAE
# Use Brute-force search algorithm to find the maximum value of likelihood function
rranges = (0, pi/2, pi/200) # Range of grid for Brute-force algorithm
resbrute = optimize.brute(likelihood_vqae, (rranges,), args=params, full_output=True, finish=optimize.fmin) # Call Brute-force algorithm
theta_a = resbrute[0][0] # Theta corresponds to the minimum of -f
amp_VQAE = np.sin(theta_a) ** 2 # Quantum amplitude estimation from VQAE
error_VQAE = abs(amp_VQAE - quantum_amp) # Absolute estimation error
rate_VQAE = error_VQAE/quantum_amp # Relative estimation error
print("=================================")
print(f"The maximum value for likelihood function is {-resbrute[1]} when theta = {resbrute[0][0]} rad")
print(f"VQAE result is {amp_VQAE}, absolute error is {error_VQAE}, relative error is {100 * rate_VQAE}%")
================================= The maximum value for likelihood function is -728.8282960799222 when theta = 0.5310066244864633 rad VQAE result is 0.2564425882363815, absolute error is 0.006442588236381497, relative error is 2.5770352945525987%
As shown above, VQAE algorithm not only achieves amplitude estimation with high accuracy, but also has evidently shallower quantum circuit compared with original MLAE algorithm. The depth of quantum circuit in VQAE is defined by the sequence of MLAE and the variational period. For example, for a circuit with $M = 50$ and variational period of 5. The depth of VQAE is about $\sim 1/10$ of MLAE. In this way, VQAE can be more promising to be implemented on NISQ hardware compared to MLAE.
The quantum query complexity of VQAE algorithm consists of sampling complexity $N_{samp}$ and variational complexity $N_{var}$. $$ N = N_{var} + N_{samp}, $$ $$ N_{var} = N_{var/1}(2k+2)\lfloor M/k \rfloor \sim O(k\lfloor M/k \rfloor), $$ $$ N_{samp} = hk(k+2)\lfloor M/k \rfloor + h(M\%k)(M\%k+2), $$ where $M$ is the maximum of linear increment sequence, $k$ is the variational period of VQAE, $h$ is the number of repeated sampling for each state. $N_{var/1}=2n_fn_sn_p$ is the number of circuits needed to be run for each variational update, where $n_p$ is the number of parameters of a parameterized quantum circuit (PQC), $n_s$ is the total number of sweeps through all the parameters of the PQC, and $n_f$ is the number of Bernoulli trials per evaluation of the objective function ($\sim n_s$). The factor 2 comes from the fact that two evaluations of the objective function are required for each evaluation of the gradient. For detailed explanation, please refer to [1].
# Calculate the quantum query complexity of VQAE
from math import floor
M_vqae = M
k_cycle = cycle
n_p = theta_size
n_s = ITR
n_f = n_s
N_var1 = 2 * n_p * n_s * n_f
N_var = N_var1 * (2 * k_cycle + 2) * floor(M_vqae/k_cycle)
N_samp = N_k_vqae * k_cycle * (k_cycle + 2) * floor(M_vqae/k_cycle) + N_k_vqae * (M_vqae % k_cycle) * (M_vqae % k_cycle + 2)
print(f"Sampling complexity is {N_samp}")
print(f"Variational complexity is {N_var}")
print(f"Quantum query complexity for VQAE is {N_var + N_samp}")
Sampling complexity is 8750 Variational complexity is 180000000 Quantum query complexity for VQAE is 180008750
We notice the quantum query complexity of VQAE is large, and mainly contributed from the complexity of variational approximation process. There is a trade-off between complexity from the depth of quantum circuit and variatonal process. However, there exists some design of the variational process to decrease the variational complexity. For example, adaptive VQAE mentioned in [1].
Summary¶
The tutorial first reviews the quantum amplitude estimation problem and its difficulty. Then maximum likelihood amplitude estimation(MLAE), which avoids quantum phase estimation, is reviewed. However, the circuit of MLAE can be too deep to be implemented by NISQ hardware. To decrease the depth of circuit of MLAE, variational quantum amplitude estimation (VQAE) is developed based on MLAE. The variational approximation process in VQAE keeps the depth below a constant number. Therefore, VQAE increases the probability of realizing quantum amplitude estimation on NISQ hardware. Also, it's necessary to notice that variational process will introduce variational complexity. Thus, there is a tradeoff between variational process and the depth of quantum circuit.
The tutorial implements single-qubit MLAE and VQAE based on Paddle Quantum, and demonstrates high-accuracy estimation of the preset quantum amplitude. Furthermore, the tutorial compares the relation of estimation error and quantum query complexity between MLAE and Classical Monte-Carlo method, and shows the quantum speedup effect by numerical experiment results.
References¶
[1] Plekhanov, Kirill, et al. "Variational quantum amplitude estimation." Quantum 6 (2022): 670. https://quantum-journal.org/papers/q-2022-03-17-670/
[2] Preskill, John. "Quantum computing in the NISQ era and beyond." Quantum 2 (2018): 79. https://quantum-journal.org/papers/q-2018-08-06-79/
[3] Suzuki, Yohichi, et al. "Amplitude estimation without phase estimation." Quantum Information Processing 19.2 (2020): 1-17. https://link.springer.com/article/10.1007/s11128-019-2565-2
[4] Brassard, Gilles, et al. "Quantum amplitude amplification and estimation." Contemporary Mathematics 305 (2002): 53-74. https://arxiv.org/pdf/quant-ph/0005055.pdf