Variational Quantum Eigensolver

Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.

Overview

It is widely believed that one of the most promising applications of quantum computing in the near future is solving quantum chemistry problems [1-2]. Variational Quantum Eigensolver (VQE) is a strong proof to this possibility of studying quantum chemistry with Noisy Intermediate-Scale Quantum (NISQ) devices [1-4]. The core task is to solve the ground state of any molecular Hamiltonian $\hat{H}$ by preparing a parametrized wave function ansatz $|\Psi(\boldsymbol\theta)\rangle$ on a quantum computer and adopt classical optimization methods (e.g. gradient descent) to adjust the parameters $\boldsymbol\theta$ to minimize the expectation value $\langle \Psi(\boldsymbol\theta)|\hat{H}|\Psi(\boldsymbol\theta)\rangle$. This approach is based on the Rayleigh-Ritz variational principle.

$$ E_0 = \min_{\boldsymbol\theta} \langle \Psi(\boldsymbol\theta)|\hat{H}|\Psi(\boldsymbol\theta)\rangle. \tag{1} $$

where $E_0$ denotes the ground state energy. Numerically, it can be understood as finding the smallest eigenvalue $\lambda_{\min}$ of a discretized Hamiltonian $H$ (hermitian matrix) and its corresponding eigenvector $|\Psi_0\rangle$. How such a discretization can be done on a classical computer belongs to the art of quantum chemistry and is far beyond the scope of this tutorial. We will discuss this part with a few words in the background section. In general, such a Hamiltonian $H$ is expressed as a weighted sum of Pauli spin operators $\{X,Y,Z\}$ (native to quantum devices) such that this information can be processed on a quantum computer.

$$ H = \sum_k c_k ~ \bigg( \bigotimes_{j=0}^{M-1} \sigma_j^{(k)} \bigg), \tag{2} $$

where $\sigma_j^{(k)} \in \{I,X,Y,Z\}$ and $M$ stands for qubit number. We refer this form of Hamiltonian as Pauli strings. For example,

$$ H= 0.12~Y_0 \otimes I_1-0.04~X_0\otimes Z_1. \tag{3} $$

In the next section, we will provide a brief review on the electronic structure problem which essentially tells us how to calculate the Hamiltonian $H$. For those who are already familiar with this topic or only interested in how to implement VQE on Paddle Quantum, please skip this part and jump into the illustrative example of hydrogen molecule $H_2$.

Background: the electronic structure problem

In this section, we focus on one of the fundamental problems in quantum chemistry -- the electronic structure problem. To be more specific, we are interested in the low lying energy eigenstates of any given molecule. These knowledge could help predict reaction rates and location of stable structures [5]. Suppose a molecule consists of $N_n$ nuclei and $N_e$ electrons, the first quantized (canonical quantization) Hamiltonian operator $\hat{H}_{mol}$ describing the total energy of this molecular system can be written as

$$ \begin{align} \hat{H}_{\text{mol}} & = -\sum_{i}\frac{\nabla_{R_i}^2}{2M_i} - \sum_{i} \frac{\nabla_{r_i}^2}{2} -\sum_{i,j}\frac{Z_i}{\lvert R_i - r_j\lvert} + \sum_{i,j>i}\frac{Z_iZ_j}{\lvert R_i - R_j\lvert} + \sum_{i, j>i}\frac{1}{\lvert r_i - r_j\lvert}, \tag{4} \end{align} $$

where $R_i, M_i,$ and $Z_i$ denote the position, mass and atomic number (the number of protons) of the $i^{th}$ nucleus, and the positions of electrons are $r_i$. The first two sums describe the kinetic energy of nuclei and electrons, respectively. The third sum describes the attractive Coulomb interaction between the positively charged nuclei and the negatively charged electrons. The last two terms represent the repulsive nuclei-nuclei and electron-electron interactions. Here, the molecular Hamiltonian $\hat{H}_\text{mol}$ is already in atomic units of energy, Hartree. $1$ Hartree is $[\hbar^2/(m_ee^2a_0^2)] = 27.2$ eV or $630$ kcal/mol, where $m_e, e,$ and $a_0$ stand for the mass of electron, charge of electron, and Bohr radius.

Note: The spin-orbit interaction and hyperfine interaction are not considered in this picture. They can be treated as perturbations if necessary.

Born-Oppenheimer approximation

Since the nuclei are much heavier than electrons, the electrons will move much faster than the nuclei. It is reasonable to treat the positions of nuclei as fixed, $R_i =$ constants. This is known as the Born-Oppenheimer approximation by decoupling the behavior of nuclei and electrons in time scale. Consequently, the kinetic energy term of nuclei will disappear and the nuclei-nuclei repulsive interaction term can be viewed as an energy shift (independent of electron positions $r_i$). We could derive the electronic Hamiltonian $\hat{H}_{\text{electron}}$ as

$$ \begin{align} \hat{H}_{\text{electron}} & = - \sum_{i} \frac{\nabla_{r_i}^2}{2} -\sum_{i,j}\frac{Z_i}{\lvert R_i - r_j\lvert} + \sum_{i, j>i}\frac{1}{\lvert r_i - r_j\lvert} \tag{5}, \end{align} $$

The energy levels of the electrons in the molecule can be found by solving the time independent Schrödinger equation

$$ \hat{H}_{\text{electron}} |\Psi_n \rangle = E_n |\Psi_n \rangle, \tag{6} $$

where $n$ stands for the energy level. Notice the electron repulsion terms scale as $N_e(N_e-1)/2$ which means for the Oxygen molecule $O_2$ carrying 16 electrons there will be 120 electron repulsion terms in total! In general, this problem cannot be solved analytically. As Dirac concluded in Quantum mechanics of many-electron systems [6],

The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.

​ -- Paul Dirac (1929)

A straightforward numerical approach is discretizing the infinite-dimensional Hilbert space into equidistant grid points where linear algebra guides the whole calculation. Suppose each axis of space is discretized into $k$ points, the $N$-electron (drop the subscript e for simplicity) wave function can be written as [2]

$$ |\Psi \rangle = \sum_{\mathbf{x_1}, \ldots, \mathbf{x_N}} \psi(\mathbf{x_1}, \ldots, \mathbf{x_N}) \mathcal{A}(|\mathbf{x_1}, \ldots, \mathbf{x_N}\rangle). \tag{7} $$

where coordinate $|\mathbf{x_j}\rangle = |r_j\rangle |\sigma_j\rangle$ records the spatial location and spin of the $j^{th}$ electron, $|r_j\rangle = |x_j,y_j,z_j\rangle$ for $j\in \{1,2,\cdots,N\}$, $x_j,y_j,z_j \in \{0,1,\cdots,k-1\}$ and $\sigma_j \in \{\downarrow,\uparrow\}$ for spin down or up. There will be $k^{3N}\times 2^{N}$ complex amplitudes in total. Here, $\mathcal{A}$ denotes anti-symmetrization and a consequence of the Pauli exclusion principle (electrons are fermion), and $\psi(\mathbf{x_1}, \mathbf{x_2}, \ldots, \mathbf{x_N})=\langle\mathbf{x_1}, \mathbf{x_2}, \ldots, \mathbf{x_N}|\Psi\rangle$. One can see that storing such a wave function already requires exponentially growing memory with respect to the number of electrons $N$. This would make classical simulation methods based on this naive numerical approach intractable for systems size larger than few tens of electrons. Now, the question becomes can we prepare such a wave function $|\Psi\rangle$ directly on a quantum computer and measure the expectation value $E_0$? In the next section, let's take the simplest molecular system -- hydrogen molecule $H_2$ as a concrete example.

Note: A detailed review on quantum chemistry and existing classical computational methods are far beyond the scope of this tutorial, we refer the enthusiastic readers to the standard textbooks 'Molecular Electronic-Structure Theory' [5] by Helgaker and 'Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory' [7] by Szabo & Ostlund. To bridge to knowledge gap between quantum chemistry and quantum computing, please check the following review papers Quantum computational chemistry [2] and Quantum Chemistry in the Age of Quantum Computing [1].

Note: For energy calculation, it is desired to reach the chemical accuracy of $1.6\times10^{-3}$ Hartree or 1 kcal/mol .

Ground state of the hydrogen molecule $H_2$

Building electronic Hamiltonian

First of all, let us import the necessary libraries and packages. qchem module in Paddle Quantum is developed on top of openfermion, and currently, its quantum chemistry backend is PySCF so you need to install these two packages before executing the following codes (NOTE: PySCF only support Mac and Linux platform, we are adding support for more quantum chemistry backends, and will improve our support for Windows in our next release). We strongly encourage you to read the tutorial Building molecular Hamiltonian first, which introduces how to utilize our quantum chemistry toolkit qchem.

Note: As to the environment setting, please refer to README.md.

import paddle
import paddle_quantum
import paddle_quantum.qchem as qchem
from paddle_quantum.loss import ExpecVal
from paddle_quantum import Hamiltonian
from paddle_quantum.state import zero_state, State
from paddle_quantum.ansatz import Circuit
from paddle_quantum.linalg import dagger
from paddle_quantum import Backend

import os
import matplotlib.pyplot as plt

import numpy
from numpy import pi as PI
from numpy import savez, zeros

# Eliminate noisy python warnings
import warnings
warnings.filterwarnings("ignore")

/usr/local/Caskroom/miniconda/base/envs/pq_new/lib/python3.8/site-packages/paddle/tensor/creation.py:125: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. 
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
  if data.dtype == np.object:
/usr/local/Caskroom/miniconda/base/envs/pq_new/lib/python3.8/site-packages/paddle/tensor/creation.py:125: DeprecationWarning: `np.object` is a deprecated alias for the builtin `object`. To silence this warning, use `object` by itself. Doing this will not modify any behavior and is safe. 
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
  if data.dtype == np.object:

To analyze specific molecules, we need several key information such as geometry, basis set (such as STO-3G), multiplicity, and charge to model the molecule and to calculate its one-body integral, two-body integral and the Hamiltonian. We can use Molecule class provided by qchem in Paddle Quantum to easily obtain molecular Hamiltonian stored as Paddle Quantum's Hamiltonian object. This will facilitates our further operations.

mol = qchem.Molecule(
    geometry=[('H', [-0., 0., 0.0]), ('H', [-0., 0., 0.74])],   # Molecular geometry
    basis="sto-3g",                                             # Basis set
    multiplicity=1,                                             # Spin multiplicity
    charge=0,                                                   # Total charge
    driver=qchem.PySCFDriver()                                  # Quantum chemistry engine
)
# extract Hamiltonian
molecular_hamiltonian = mol.get_molecular_hamiltonian()

# print result
print("\nThe generated h2 Hamiltonian is \n", molecular_hamiltonian)

converged SCF energy = -1.11675930739643

The generated h2 Hamiltonian is 
 -0.0970662681676312 I
0.1714128264477692 Z0
0.17141282644776926 Z1
-0.22343153690813466 Z2
-0.22343153690813466 Z3
0.16868898170361213 Z0, Z1
0.12062523483390417 Z0, Z2
0.16592785033770344 Z0, Z3
0.16592785033770344 Z1, Z2
0.12062523483390417 Z1, Z3
0.1744128761226159 Z2, Z3
-0.04530261550379927 X0, X1, Y2, Y3
0.04530261550379927 X0, Y1, Y2, X3
0.04530261550379927 Y0, X1, X2, Y3
-0.04530261550379927 Y0, Y1, X2, X3

Note: This Hamiltonian is generated with an interatomic distance of $d = 74$ pm.

In addition to inputting molecular geometry directly, inputting molecular geometry file (.xyz file) is also allowed. For more information about quantum chemistry toolkit, please refer to the tutorial Building molecular Hamiltonian. If you need to test the geometric configuration of more molecules, please check out this database.

Building QNN and trial wave function

To implement VQE, we firstly need to design a quantum neural network QNN to prepare the wave function ansatz $|\Psi(\boldsymbol\theta)\rangle$. Here, we provide a 4-qubit quantum circuit template with a depth of $D$ blocks. The dotted frame in the figure below denotes a single block:

Next, we use the Circuit class and the built-in real_entangled_layer() circuit template in Paddle Quantum to realize this QNN.

def U_theta(num_qubits: int, depth: int) -> Circuit:
    """
    Quantum Neural Network
    """
    
    # Initialize the quantum neural network according to the number of qubits N
    cir = Circuit(num_qubits)
    
    # Built-in {R_y + CNOT} circuit template
    cir.real_entangled_layer(depth = depth)
    
    # Lay R_y gates in the last row
    cir.ry()
        
    return cir

Setting up the loss function and model

Now that we have the target Hamiltonian and QNN, we will further define the training model and loss function. By applying the QNN $U(\theta)$ on the initial state $|0..0\rangle$, we get the output state $|\psi(\boldsymbol\theta)\rangle $. Then, the loss function to be minimized is the expectation value,

$$ \min_{\boldsymbol\theta} \mathcal{L}(\boldsymbol \theta) = \min_{\boldsymbol\theta} \langle \Psi(\boldsymbol\theta)|H |\Psi(\boldsymbol\theta)\rangle = \min_{\boldsymbol\theta} \sum_k c_k~\langle \Psi(\boldsymbol\theta)| \bigotimes_j \sigma_j^{(k)}|\Psi(\boldsymbol\theta)\rangle. \tag{8} $$

# Define loss function
loss_func = ExpecVal(molecular_hamiltonian)

Hyper-parameters

Before training the QNN, we also need to set some training hyper-parameters, mainly the learning rate (LR), the number of iterations (ITR), and the depth (D) of repeated blocks.

ITR = 80  # Set the number of optimization iterations
LR = 0.4   # Set the learning rate
D = 2      # Set the depth of the repetitive calculation module in QNN
N = molecular_hamiltonian.n_qubits # Set number of qubits

Training

After all the training model parameters are set, we convert the data into Tensor in the Paddle, and then train the quantum neural network. The results of the training process is stored in the summary_data file.

# Determine the parameter dimensions of the network 
cir = U_theta(N, D)

# In general, we use the Adam optimizer to obtain relatively good convergence,
# Of course you can change it to SGD or RMS prop.
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=cir.parameters())

# Define initial state
init_state = zero_state(N)

# Record optimization results
summary_iter, summary_loss = [], []

# Optimize iterations
for itr in range(1, ITR + 1):

    # Forward propagation calculates the loss function
    state = cir(init_state)
    loss = loss_func(state)
    # Back propagation minimizes the loss function
    loss.backward()
    opt.minimize(loss)
    opt.clear_grad()

    # Update optimization results
    summary_loss.append(loss.numpy())
    summary_iter.append(itr)

    # Print results
    if itr % 20 == 0:
        print("iter:", itr, "loss:", "%.4f" % loss.numpy())
        print("iter:", itr, "Ground state energy:", "%.4f Ha" 
                                            % loss.numpy())
    if itr == ITR:
        print("\nCircuit after training:") 
        print(cir)

# Save the training results in the Output folder
os.makedirs("output", exist_ok=True)
savez("./output/summary_data", iter = summary_iter, 
                               energy=summary_loss)

iter: 20 loss: -1.0850
iter: 20 Ground state energy: -1.0850 Ha
iter: 40 loss: -1.1306
iter: 40 Ground state energy: -1.1306 Ha
iter: 60 loss: -1.1364
iter: 60 Ground state energy: -1.1364 Ha
iter: 80 loss: -1.1371
iter: 80 Ground state energy: -1.1371 Ha

Circuit after training:
--Ry(7.897)----*--------------x----Ry(1.523)----*--------------x----Ry(3.116)--
               |              |                 |              |               
--Ry(1.603)----x----*---------|----Ry(4.714)----x----*---------|----Ry(4.633)--
                    |         |                      |         |               
--Ry(6.198)---------x----*----|----Ry(1.801)---------x----*----|----Ry(4.580)--
                         |    |                           |    |               
--Ry(6.146)--------------x----*----Ry(1.552)--------------x----*----Ry(3.128)--
                                                                               

Benchmarking

We have now completed the training of the quantum neural network, and the estimated value of the ground state energy obtained is $E_0 \approx -1.137 $ Hartree. The estimation obtained with VQE is consistent with the value of the ground state energy $E_0 = -1.13728$ Hartree calculated by psi4 at sto-3g basis using the full configuration-interaction (FCI) method within the chemical accuracy $\varepsilon = 1.6 \times 10^{-3}$ Hartree.

result = numpy.load('./output/summary_data.npz')

eig_val, eig_state = numpy.linalg.eig(
                     molecular_hamiltonian.construct_h_matrix())
min_eig_H = numpy.min(eig_val.real)
min_loss = numpy.ones([len(result['iter'])]) * min_eig_H

plt.figure(1)
func1, = plt.plot(result['iter'], result['energy'], 
                  alpha=0.7, marker='', linestyle="-", color='r')
func_min, = plt.plot(result['iter'], min_loss, 
                  alpha=0.7, marker='', linestyle=":", color='b')
plt.xlabel('Number of iteration')
plt.ylabel('Energy (Ha)')

plt.legend(handles=[
    func1,
    func_min
],
    labels=[
        r'$\left\langle {\psi \left( {\theta } \right)} '
        r'\right|H\left| {\psi \left( {\theta } \right)} \right\rangle $',
        'Ground-state energy',
    ], loc='best')
plt.text(-15.5, -1.145, f'{min_eig_H:.5f}', fontsize=10, color='b')
#plt.savefig("vqe.png", bbox_inches='tight', dpi=300)
plt.show()

Determining the interatomic distance

Recall the above calculation is done with an interatomic distance $d = 74$ pm between two hydrogen atoms. Another interesting aspect we can try with VQE is determining the true interatomic distance by modifying the h2.xyz file. The results are summarize in figure below,

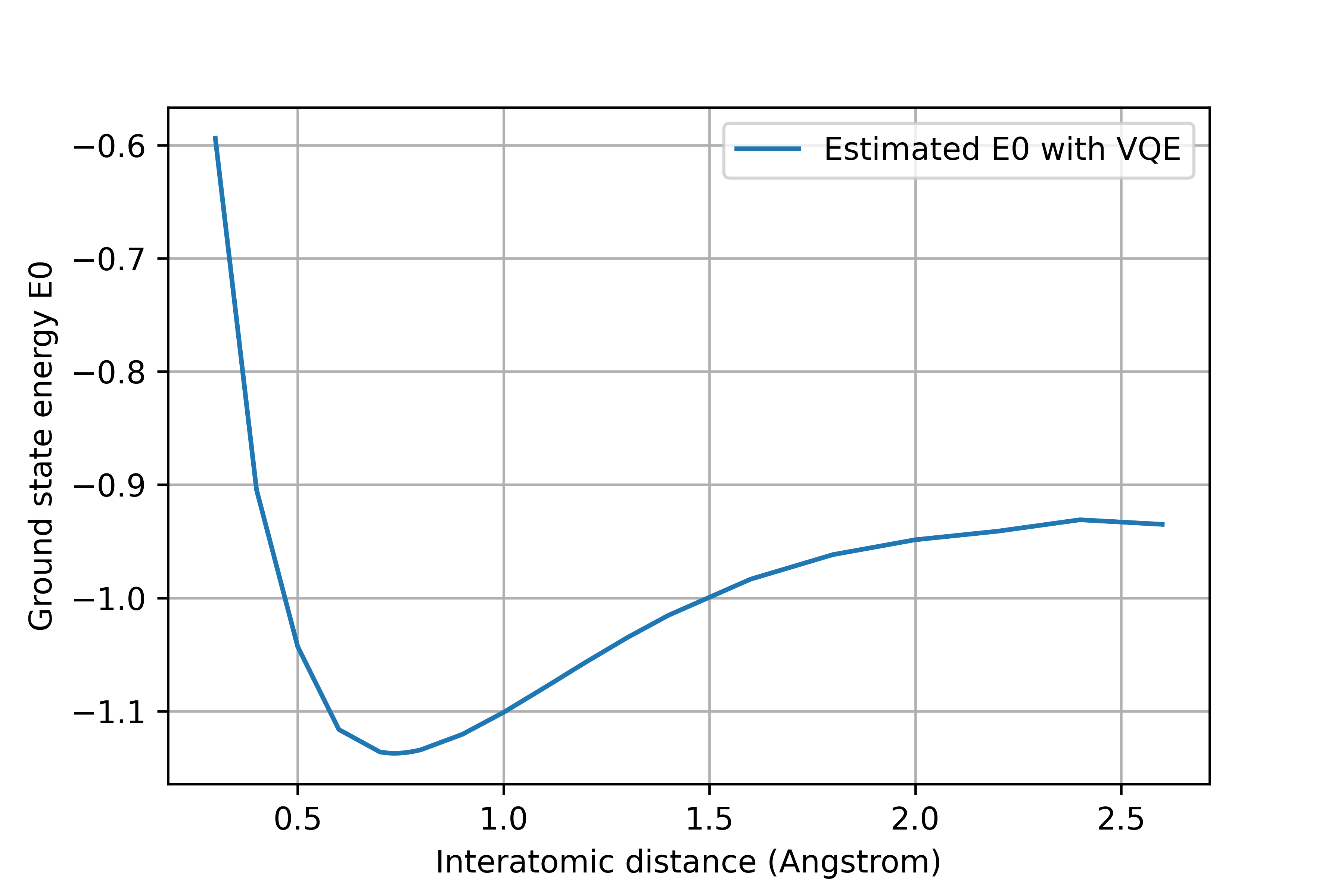
The lowest value is found around $d = 74$ pm (1 pm = $1\times 10^{-12}$m), which is consistent with the experimental data $d_{exp} (H_2) = 74.14$ pm.

---

References

[1] Cao, Yudong, et al. Quantum Chemistry in the Age of Quantum Computing. Chemical reviews 119.19 (2019): 10856-10915.

[2] McArdle, Sam, et al. Quantum computational chemistry. Reviews of Modern Physics 92.1 (2020): 015003.

[3] Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).

[4] Moll, Nikolaj, et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Science and Technology 3.3 (2018): 030503.

[5] Helgaker, Trygve, Poul Jorgensen, and Jeppe Olsen. Molecular electronic-structure theory. John Wiley & Sons, 2014.

[6] Dirac, Paul Adrien Maurice. Quantum mechanics of many-electron systems. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 123.792 (1929): 714-733.

[7] Szabo, Attila, and Neil S. Ostlund. Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation, 2012.